이번 포스팅은 베이지안 방식을 기반으로한 회귀분석 풀이법 중 하나인 Gaussian Process을 다룬다. 먼저 회귀분석(regression)을 많이 접해본 이들은 통계적인 추론방식등을 이용해서 아래와 같은 문제를 많이 접해봤으리라 믿는다.

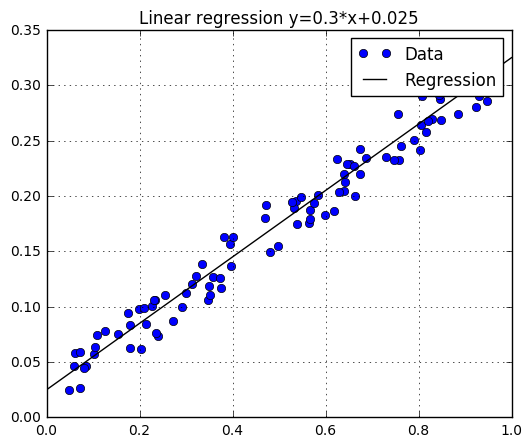
위 그림에서 데이터인 푸른점들을 선형식, $y=ax+b$ 형태로 가정하고 데이터 $(x,y)$값을 이용해서 $a$와 $b$인 계수를 구하는 공식에 대입하면 끝인 문제이다. 아마 대학교 학부수준에서는 기초통계 수업을 들으면 최소한 한번씩은 접해봤을 문제였을 것이고 위와 같은 문제를 해결하는데 큰 거부감이 없을것이다.

자, 위 회귀분석 문제의 핵심은 ‘1. 선형방정식을 따른다’와 ‘2. 선형방정식을 이루는 계수를 구하면 문제해결’이라는 것이다. 이와 같은 문제해법은 Parameteric Method의 전형적인 방식이다. 하지만 우리는 이 단순한 형태의 문제만이 아닌, 더 어렵고 복잡하고 실전에 맞는 문제를 해결할 능력이 필요하다. 변수가 많아지고, 데이터의 형태가 ‘선형’이 아니고, 방정식을 이루는 계수가 많아지고 구하기가 까다로워 지면 Parametric Method보다는 Non-Parametric Method가 더욱 효과적인 방식으로 해결전략을 세우는 것이 바람직하다. 바로 Gaussian Process가 Non-Parametric Method 회귀분석의 대표예시가 된다. Gaussian Process는 대부분의 베이지안 방식이 그렇듯 많은 수학개념이 필요하기 때문에 하나하나 필요한 배경지식에 대해서 소제목으로 나누어서 다루어 보겠다.

Gaussian Distribution

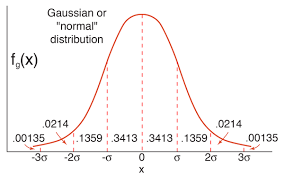
자연계에서 가장 많이 나타나는 확률분포표이다. 돈이 많은 사람의 비율-돈이 많은사람의 비율, 공부를 못하는사람-잘하는 사람의 비율 등등 무엇인가 차이가 나는 표본들이 분포한 그림으로써 특이한 사람들은 소수고 중간에 있는 표본들이 많은 그림을 보여주는 그림으로 많이 알고있는 그림이다. 그런데 Gaussian Process를 알기 위해서는 분포표의 수식과 성질을 어느정도 숙지할 필요가 있다.

• 1D Gaussian distribution

\(\mathcal{N}({x} \vert \mu,\sigma) = \frac{1}{\sqrt{2\pi\sigma^{2}}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right).\) (1)

미리 말하지만, 1D와 2D gaussian distiribution 그림은 필자가 직접그린 것이 아닌 구글에서 이미지를 그냥 가지고 왔다. 1D상황의 분포는 분포의 평균($\mu$)에서 가장 위로 볼록하게 나타나며 분산값($\sigma$)이 커질수록 마치 반죽이 펼쳐지듯 퍼지는 형태의 그림이 된다. 분산값이 크다는 이야기는 표본 각각이 평균으로 부터 멀리 떨어져 있음을 보이므로 표본 집단의 성질을 평균으로 정의내리기 어렵다는 의미가 된다. 모평균추정을 하부 섹션으로 만들어서 이야기 해보겠다. 돌아와서 평균과 분산값은 1D 상황이므로 더 말할필요 없이 스칼라 형태의 텐서다.

• Multi-Dimension Gaussian distribution

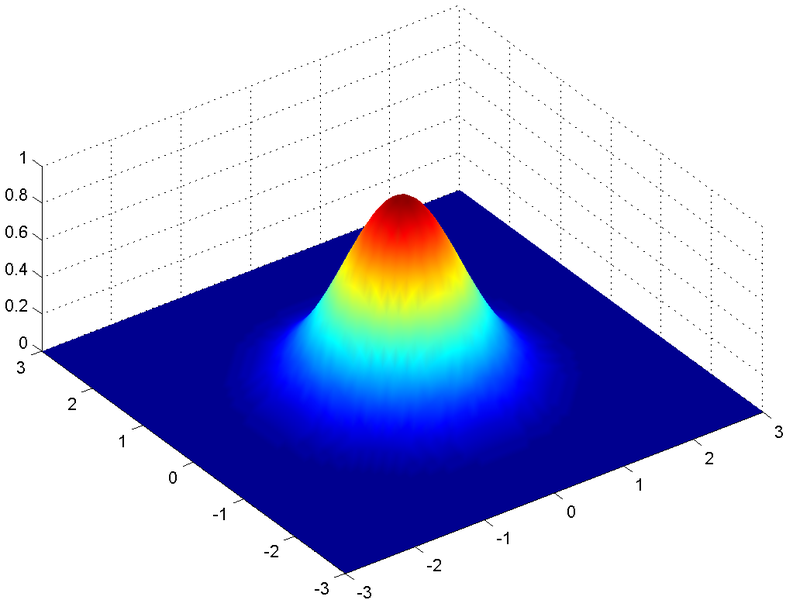
\(\mathcal{N}({X} \vert \mu,\Sigma) = \frac{1}{(2 \pi)^{d/2}}{\vert\Sigma\vert}^{-1/2}exp\left(-\frac{1}{2}(X-\mu)\vert\Sigma\vert^{-1}(X-\mu)^T \right).\) (2)

다차원의 gaussian distribution은 조금 생소할수 있다. 무엇이든 차원을 확장하는 첫 단계가 생소하고 어렵듯 1D에서 2D로 넘어가는 과정도 조금 어색할지도 모르겠다. 함수 형태가 볼록하고 펴지고 하는 모습들은 1D에서의 형태와 크게 다를바가 없다. 다만, 변수 $X$와, 평균 $\mu$는 여기에서 $d$차원의 벡터이며, 분산(정확히 공분산행렬) $\Sigma$은 $d \times d$행렬이 된다. 공분산 행렬은 입력변수의 차원간의 상관관계를 표현한 분산으로 자세한 개념은 Andrew Ng 교수님의 강의를 참조하면 좋겠다.

Inference about a Population Mean

다음 살펴봐야 할 부분은 모평균의 추정개념이다. 알고있다면 과감히 패스하시고 아니면, 고등학교 교과과정에서 다루는 내용이지만 개념을 잊어버렸을 독자들을 위하여 간단하게 요약하고 넘어가는 부분이니 감안하기를 바란다. 1D gaussian distribution의 식 (1)에서 평균과, 분산값을 알고 있다면 우리는 샘플의 분포를 그릴 수 있다. 하지만 역으로 일부의 샘플을 통해서 역으로 모집단의 평균,분산을 어느정도 예측할수 있지 않을까하는 의문을 삼을 수 있다. 선거철에서 흔히 뉴스에서 나오는 ‘표본 몇명을 대상으로 95퍼센트의 신뢰도로 어느 후보가 앞선다’는 식의 조사가 바로 모평균의 추정이다. 우선 Gaussian distribution의 Probability Density Function(PDF)값들을 적분한 값은 1이라는 것을 인지하고, 평균으로 부터 1$\sigma$, 2$\sigma$ 등의 값으로 좌우로 샘플되는 구간들이 있다. 특별한 숫자지만 $\sigma$의 1.96배수와, 2.58배수로 좌우로 펼쳐진 구간의 적분면적은 각각 0.95, 0.99값이 나온다(95%, 99%). 글로 해석해보면 샘플 변수 $x$가 평균으로부터 $-1.96\sigma \sim +1.96\sigma$의 구간으로 있다면 전체 샘플링 영역의 95%구간안에 속해있다고 표현하는 것이다.

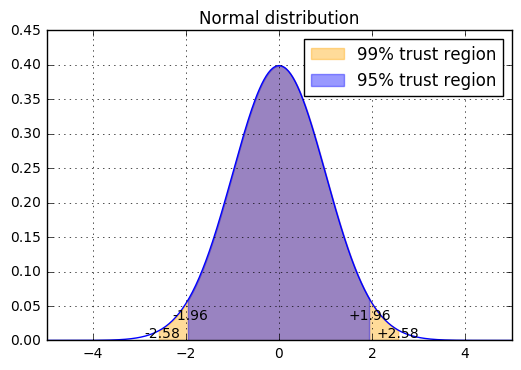
그렇다면 평균이 0이고 분산값이 1인 표준정규분포(Unit gaussian distribution)에서 신뢰구간을 생각해보자. $\sigma$값이 1이므로 95%의 샘플링 변수($z$) 신뢰구간은 평균값으로부터 $-1.96~1.96$이며 이를 식으로 표현하면 다음과 같다.

\(P\left(-1.96 \leq z \leq 1.96\right)=\frac{95}{100}.\) (3)

위 문단에서 썼던 $\sigma$의 1.96배수로 구한 95%신뢰 구간의 의미를 식(3)으로 표현하였다. 여기서 표준정규분포(평균이 0이고 분산이 1인 gaussian distribution)의 변수 $Z$가 나왔는데 이는 우리가 식(1)에서 사용했던 변수 $X$와는 다음과 같은 관계를 가지고 있다.

\(z = \frac{x-\mu}{\sigma/\sqrt{n}}.\) (4)

그러므로, 식(4)를 $x$에 대해서 풀어보면 아래와 같다.

\(x = \mu+z*\frac{\sigma}{\sqrt{n}}.\) (5)

따라서, 샘플링 변수 $x$가 $n$개수 만큼 샘플링되었을때 95%의 신뢰도로 어떤 값($\mu$)을 추정한다는 의미는 아래 수식으로 표현된다.

\(P\left(\mu-1.96\frac{\sigma}{\sqrt{n}} \leq x \leq \mu+1.96\frac{\sigma}{\sqrt{n}} \right) = 0.95.\)(6)

일반적으로 Gaussian Process가 지금까지 살펴본 모평균의 추정 과정과 맥락이 동일하다. 추론하고자 하는 함수값이 곧 모평균의 추정으로 얻은 $\mu$값이며, 추정의 신뢰도를 구할수 있는 $\sigma$값도 계산을 통해서 얻을수 있게 된다. 위 그림에서 데이터 몇 개를 이용해 GP를 계산하면 함수값과 그에 대한 추정 신뢰구간이 범위형태로 그려지는 것을 볼 수 있다. 참고로 위 그림은 함수값이 정답안에 있을 확률이 95%의 신뢰구간이라고 ML이 표현하는 것을 의미한다. 이제 Gaussian Process의 추정과 신뢰구간이라는 개념을 살펴보았으니 이 둘을 어떻게 계산하는지 보다 면밀하게 짚고 넘어 가도록 하겠다. 다음 문단부터 필수 개념인 Kernel에 대해서 살펴보도록 하겠다.

Kernel

Kernel이 하는 역할을 먼저 알아보도록 하겠다.

• Kernel 1기능: Mapping 수학에서 어떤 문제를 해결할 때 상변환이라는 개념을 도입한다. 직교좌표계에서 원형좌표계로 변형시킨다던가 하는 방법이다. 아래 그림을 보자. 그림처럼 구간을 분리시키고자 하지만 단칼로 한번에 구간을 분리시키기가 굉장히 어려운 문제다. 하지만 우리는 Mapping, 상변환의 개념을 통하여 데이터들을 간단하게 분리시킬 방법을 고안할수 있다. 2D공간에서만 문제를 생각하지말고 3D공간으로 바꾸어 문제를 풀어볼수 있다. Kernel 내부에는 mapping함수가 존재해서 그림과 같이 데이터가 복잡하게 분포하고 있더라도 우리가 선택한 바대로 데이터 상변환을 통해 풀기 쉽게 바꿔 버릴 수 있다.

• Kernel 2기능: Inner product 첫번째의 Mapping만 한다면 Kernel은 반쪽짜리 역할밖에 하지 못한다. kernel은 두개의 벡터를 입력변수로 삼고 둘을 Inner product연산을 통해서 스칼라 값으로 변화하여 다른 차원의 개념으로 변화를 한다. 수식으로 표현하면 다음과 같은 모양이 된다.

\(\begin{align} K(x_1, x_2) &= <\phi(x_1), \phi(x_2)> \\ &= \phi(x_1)^T\phi(x_2). \end{align}\) (7)

즉, Kernel의 기능을 풀어쓰면 입력받은 두 변수를 1) 복잡하게 얽혀진 데이터를 풀기쉽도록 상 변환을 하고, 2) Inner product를 취해서 단일 스칼라 값으로 변환을 한다. 그래서 입력받은 두 변수를 추상적인 어떠한 스칼라로 변환을 하는데 간략히 표현하면 두 입력 변수간의 유사도(Similarity)를 측정하는데 주로 이용된다. 각론으로 살펴보자면 Kernel함수로 이용되는 형태는 RBF, Step function, Linear function들로 구성되는데 Gaussian Process에서는 주로 RBF kernel이 주로 이용된다. 식 (7)을 골자로 한 RBF식은 다음과 같다.

\(K_{RBF}(x_1, x_2) = \sigma^2 exp\left(-\frac{\left\Vert x_1-x_2 \right\Vert^2}{2l^2} \right).\) (8)

여기서 $x_1$과 $x_2$간의 similarity($\left\Vert x_1-x_2 \right\Vert^2$)를 x축으로 삼고, Kernel값을 y축으로 삼으면 개형은 대략 다음과 같이 나온다.

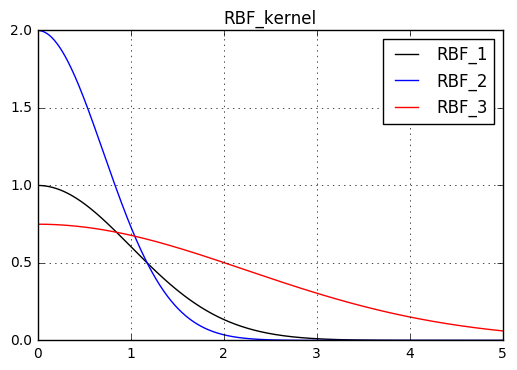
위 그림에서 $\sigma$값을 증가시키면 기준으로 삼은 RBF개형보다 $x=0$에서 더 위로 볼록한 형태의 그래프가 나오며, $l$값을 증가시키면 기준으로 삼은 RBF개형보다 더 완만한 그래프 개형이 나오게 된다. 두 그래프를 비교해서 해석하면 Kernel의 parameter인 $\sigma, l$을 어떻게 설정하는지에 따라 입력변수 $x_1, x_2$간 similarity를 강하게 판단할 것인지, 약하게 판단할것인지 척도를 kernel의 값으로 알겠다는 지표가 된다. $\sigma$값을 증가하면 입력변수 $x_1, x_2$간 similarity를 크게 파악하겠다는 의도를 반영하며, $l$값이 증가하면 입력변수 $x_1, x_2$간 similarity가 낮아도 상호간의 관계를 많이 보겠다는 의도를 반영하는 바가 된다.

나름 설명한다고 했는데 왜 갑자기 Gaussian Process를 설명하는데 이해하기 어려운 Kernel은 왜 나오는 것인지 이쯤 되면 의문을 가지게 될 것이다.

Gaussian Process

Gaussian Process를 말하는데 필요한 사전지식들은 모두 준비 되었다. 수식으로 우리가 풀고자 하는 Gaussian Process를 다시 한 번 보자.

이산적으로 우리에게 주어진 데이터가 ${f(x_1), f(x_2), f(x_3), …} $처럼 있을 때 우리가 회귀분석을 하고자 하는 $f(x)$를 구하는 공식은 확률 추정의 방식으로 다음과 같이 표현된다.

\(p(f(x) \vert f(x_1),f(x_2),f(x_3),...f(x_n))\). (9)

식 (9)는 주어진 데이터로 조건부 확률 공식으로써 $f(x)$ 및 $f(x_i), \quad \forall{i}$가 각각 독립사건으로 보면 다음과 같이 전개된다.

\(\begin{align}p(f(x) \vert f(x_1),f(x_2),...f(x_n)) &= \frac{p\left(f(x), f(x_1), f(x_2)...f(x_n) \right)}{p\left(f(x_1),f(x_2)...f(x_n) \right)} \\ &=\frac{\mathcal{N}\left(f(x), f(x_1), f(x_2)...f(x_n) \vert 0,\tilde{C} \right)}{\mathcal{N}\left( f(x_1), f(x_2)...f(x_n) \vert 0,C \right)} \\ &=\mathcal{N}\left(f(x) \vert {\mu},{\sigma}^2 \right)\end{align}.\) (10)

$where,$

\[\begin{equation*} \\ c=\begin{pmatrix} K(x_1,x_1) & K(x_1,x_2) & \cdots & K(x_1,x_n) \\ K(x_2,x_1) & K(x_2,x_2) & \cdots & K(x_2,x_n) \\ \vdots & \vdots & \ddots & \vdots \\ K(x_n,x_1) & K(x_n,x_2) & \cdots & K(x_n,x_n) \\ \end{pmatrix}, \end{equation*}\] \[\begin{equation*} \\ \tilde{c}=\begin{pmatrix} K(x,x) & K^T \\ K & C \\ \end{pmatrix} \end{equation*},\]

$and$

\[\begin{equation*} \\ K=\begin{pmatrix} K(x,x_1) \\ K(x,x_2) \\ \vdots \\ K(x,x_n) \end{pmatrix} \end{equation*}.\]

식 (10)의 최종 R.H.S에서 보다시피 우리의 목표값 $f(x)$는 Gaussian distribution이고 특별한 평균값($\mu$), 그리고 분산(${\sigma}^2$)을 구하면 Gaussian Process문제를 해결했다고 볼수 있다. 식 (10)의 L.H.S는 주어진 함수값을 이용해 우리의 목표값의 확률은 조건부 Gaussian distribution를 해결해주는 과정을 확인 할 수 있다.

여기에서 가정이 들어가는데

1. “조건부 확률 모두 평균값이 0”, 주어진 데이터 $f(x_i)$에서는 정규분포를 따른다.
2. “조건부 확률상 공분산 값은 사용자가 설정한 Kernel로 만든 Covariance matrix를 따른다”, 사용자가 분산을 튜닝가능하다.

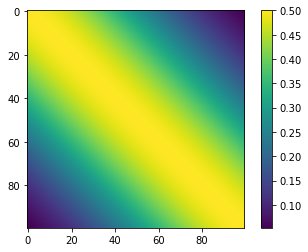
공분산 행렬값은 다음과 같이 Heatmap으로 표현된다. 각 대각행렬의 성분은 식 (10)의 첨부된 $C$의 수식처럼 RBF kernel의 동일한 원소가 입력변수로 작용하므로 최대 RBF값이 출력된다. 행렬을 수치로 보면 행-열의 인덱스 차이가 날수록 데이터간의 similarity가 줄어가므로 행렬의 원소값이 작아지는 결과를 볼 수 있다. 단, 이 작아지는 정도는 우리가 Kernel섹션에서 미리 살펴봤던 대로 사용자가 적절히 조절할수 있다. 이는 사람의 Prior knowledge가 작용하는 부분이다.

수식의 전개과정이 나름 복잡할수 있지만 전 과정을 다 생략하고 우리가 관심있어하는 부분인 $\mu$와 $\sigma$값을 정리하면 다음과 같이 쓸 수 있다.

\(\mu = K^TC^{-1}f .\) (11)

\(\sigma^{2} = K(0)-K^TC^{-1}K .\) (12)

$where,$

\[\begin{equation*} \\ f=\begin{pmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_n) \end{pmatrix} \end{equation*}.\]

(유도과정은 추후 업데이트 하도록 하겠다!)

Coding & Tutorial

GPy, [Python bayesian][https://pypi.org/project/Bayesian/] 등등 여러가지 상용 Bayesian방식을 근간으로한 Gaussian Process라이브러리들이 있지만 손으로 직접 코딩해보고 이용해보는 것이 더 본인에게 하나라도 더 와닿을 것이기에 필자가 작성해둔 Gaussian Process tutorial코드를 같이보며 샘플 문제를 같이 해결해보도록 하겠다.

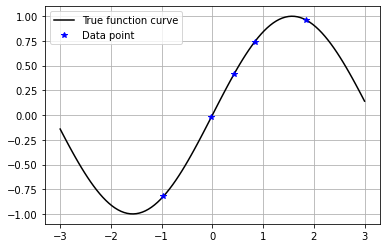
• Step 1. 데이터 세팅 위 이미지와 같이 간단한 사인파 함수에서 일부 데이터를 추출해본다

  x = np.linspace(-3,3,101)
  y = sample_function(x)
  x_data = np.array([-0.9632,-0.02,0.43287,0.839,1.8389])
  y_data = sample_function(x_data)
  

• Step 2. Kernel 세팅 RBF 함수를 이용해 Kernel을 만들어본다. (Kernel함수의 상수를 변화시키면 제각각 다른 결과가 나온다! 실험해보라)

  # define RBF kernel
  def rbf(x1,x2,sig=1,length=2):
    '''
    input 
    x1, x2 : two input data
    sig: sigma value
    length: RBF value
      
    output
    return sig**2*exp(-(x1-x2)**2/2/length**2)
    '''
    return sig**2*np.exp(-0.5*((x1-x2)/length)**2)
  

• Step 3. 식 (10)과정 구현 Gaussian Process는 평균값, 분산값만 구하면 된다. 깊이있게 알면 더 좋지만 식 (10)의 전 과정을 편하게 쓸 수 있도록 함수화한다. 처음으로, 공분산 행렬 $C$를 구현한다.

  # making mean function and covariance matrix for gaussian matrix
  def making_covariance(x_data):
    '''
    input
    x_data: len(data) array, np.ndarray
      
    output
    covariance_matrix: len(data)*len(data) matrix, np.ndarray
    '''
    covariance_matrix = np.zeros((len(x_data), len(x_data)))
    # Think covariance_matrix is positive symmetric
    for i,x_i in enumerate(x_data):
        for j,x_j in enumerate(x_data):
            if i > j:
                pass
            covariance_matrix[i,j] = rbf(x_i,x_j)
    covariance_matrix = (covariance_matrix + covariance_matrix.T)/2
    return covariance_matrix
  

  두번째, kernel vector $K$를 구현한다.

  def making_new_kernel(x0,x_data):
    '''
    input
    x0: input point that user wants guess
    x_data: given data
      
    output
    new_k: new kernel vector len(x_data)
    '''
    new_k = np.zeros(len(x_data))
    for i in range(len(new_k)):
         new_k[i] = rbf(x0,x_data[i])
    return new_k
  

  세번째, 목표치-데이터 결합 공분산 행렬 $\tilde{C}$를 구현한다.

  def making_new_covariance(x0,x_data):
    '''
    input
    x0 : input point that user wants guess
    x_data : given data
      
    output: 
    new_covariance_matrix: (len(x_data)+1) x (len(x_data)+1) size covariance matrix
    '''
    new_covariance_matrix = np.zeros((len(x_data)+1,len(x_data)+1))
    new_covariance_matrix[1:,1:] = making_covariance(x_data)
    new_covariance_matrix[1:,0] = new_kernel(x0,x_data)
    new_covariance_matrix[0,1:] = new_covariance_matrix[1:,0]
    new_covariance_matrix[0,0] = rbf(x0,x0)
    return new_covariance_matrix
  

네번째, 위를 종합하여 평균값, 분산값을 구현한다.

def calculate_mu(kernel,covariance_matrix,y_data):
    '''
    input
    kernel: kerenel vector from given data
    covariance_matrix: covariance matrix from given data   
    y_data: given data
    
    output
    kernel.T @ inv(covariance_matrix) @ y_data
    '''
    return kernel.reshape(1,-1) @ np.linalg.inv(covariance_matrix) @ y_data

def calculate_sigma(k0, kernel,covariance_matrix):
    '''
    input
    k0: rbf kernel from input inference point
    kernel: kernel vector from given data
    covariance_matrix: covariance matrix from given data
    
    output
    simga: k0-kernel.T @ inv(covariance_matrix) @ kernel
    '''
    kernel = kernel.reshape(-1,1)
    return k0 - kernel.T @ np.linalg.inv(covariance_matrix) @ kernel

마지막, 전 과정을 간략하게 하나의 함수화

def gaussian_process(x0, x_data, y_data):
    '''
    input
    x0: infernece point data
    x_data: given data
    y_data: given label data
    
    output
    mu: inference output
    sigma: inference uncertainty
    '''    
    k0 = rbf(x0,x0)
    new_kernel = making_new_kernel(x0,x_data)
    covariance_matrix = making_covariance(x_data)
    
    mu = calculate_mu(new_kernel,covariance_matrix,y_data)
    sigma = calculate_sigma(k0,new_kernel,covariance_matrix)
    return mu, np.sqrt(sigma)

• Step 4. 추론시작 이제 구현한 Gaussian_process함수를 이용해서 우리가 원하고자 하는 목표값과 분산값을 동시에 추론한다.

y_infer, y_std = [],[]
for x0 in x:
    mu,sigma = gaussian_process(x0,x_data,y_data)
    y_infer.append(mu)
    y_std.append(sigma)
    
y_infer = np.asarray(y_infer).ravel()
y_std = np.asarray(y_std).ravel()

지금까지 결과는 y_infer, y_std변수에 저장되어있으므로 우리가 육안으로 볼 수 있도록 플롯팅 한다. 불확정성 정도는 95%의 신뢰구간을 사용하도록 1.96 sigma값을 사용한다.

plt.figure(figsize=(10,8))
plt.plot(x,y,label='True curve')
plt.plot(x_data,y_data,'ko',label='Given data')
plt.plot(x,y_infer,'r--',label='Inference')
plt.fill_between(x, y_infer-1.96*y_std, y_infer+1.96*y_std, alpha=0.3, color='green',label='Uncertainty')
plt.grid()
plt.legend()

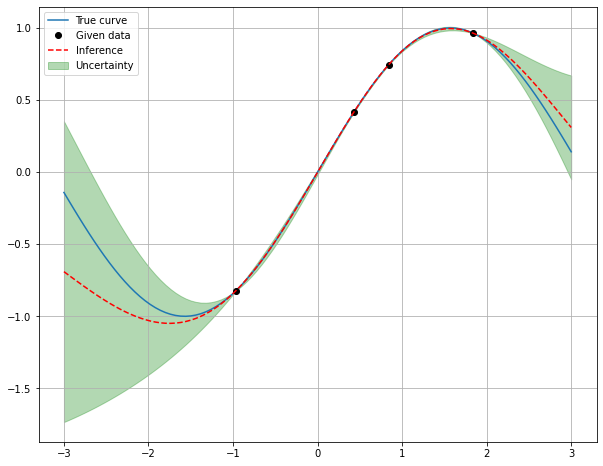
데이터가 있는 구간에서는 Machine이 확실하게 추론하여 불확정영역(녹색)이 거의 없으며, 주어진 데이터로부터 목표 추론값이 멀리 떨어질수록 불확정성 정도가 매우 크게 나타나는 것이 보인다. 신기한 점은, 단 4개의 포인트를 가지고 GP추론을 수행했는데 아주 살짝 구간에서 휘어졌다는 것을 보고서 Machine이 곡선의 사인파의 곡률을 추론했다는 점을 주목하기 바란다! 저런 수식과 단순한 데이터 4개의 포인트로 저런 정보를 추론하기엔 사람은 쉽사리 생각해보긴 어려울 것이다. 더불어 해당 문제에서는 추론값이 목표치에 아주 정확하지는 않더라도 불확정 영역안에 값들이 적중했다는 점은 상당히 고무적인 결과로 받아들이기에 충분하다고 생각한다.

(추후 GPy를 이용해서 손쉽게 문제를 푸는 방식에 대해서도 업데이트 하도록 하겠다!

Properties of Gaussian Process

이렇게 Gaussian Process를 정의내리는 과정까지 주욱 진행되었다. 아마 처음 GP에 대한 개념을 처음 접했다면, Non-Parameteric 방식에 대한 생각을 해보지 못했으리라 본다. 대부분 Machine learning을 한다고 하면 neural network를 만들고 학습 parameter를 설정하는 과정에 익숙하였겠지만 통계방식에 충실한 이런 방식에 접근하기에는 생소했을 것이다. 필자도 처음 GP를 배우며 느꼈던 점과 GP의 특징을 요약해보면 아래와 같다.

• Parameter를 따로 설정해줄 필요가 없다(장.단점 공존).
• Uncertainty를 추정 할 수 있다.(명확한 장점, Machine도 틀릴 수 있음을 실제 사람들에게 알려줘야 함)
• Prior knowledge에 상당히 좌우된다(e.g Kernel형태, 장.단점 공존).
• 데이터가 많을시 계산량이 상당히 커진다. 특별한 트릭이 없다면 데이터 개수가 $n$이면 계산량은 $O(n^3)$.(확실한 단점)
• 병렬처리 연산이 불가능하다. (데이터를 분리해서 생각할수 없음, 확실한 단점)

종합하자면 GPU보단 CPU가 성능이 좋은 환경에서, 데이터의 개수가 그리 크지 않다는 가정과, 숙달된 Machine Learning전문가가 Regression문제를 마주쳤을때 Gaussian Process를 사용하는 것이 장점으로 작용 될 수 있는 부분이다.