RL의 기본 개념부터 시작해서 TD prediction 알고리즘인 SARSA, Off-policy Q-learning까지 지난 포스팅을 통해서 살펴봤다. 많은 개념들을 다루었지만 아마 독자들은 지금까지 포스팅을 보면서 (내용을 잘 소화했다면)큰 아쉬움을 느꼈을 것이다. 바로, 예시로 든 environment들이 굉장히 정형화 되어있는 격자세계(Grid world)로 구성되었다는 점이다. 격자 환경에서 $s$가 이산화 되어있으나 실제로 풀어야 할 RL문제, 실제로 인간이 마주하고 있는 세계는 연속적인 공간으로 이루어져 있기에 이 환경에 맞도록 RL을 생각해야 한다. 이제는 agent가 인식하는 environment는 이산화된 격자가 아니며, 연속된 수로 이루어진 실제 세계에서 활동할 차례이다. 이번 포스팅에서는 이 해결전략에 대해서 다뤄보고자 한다.
Example. CartPole
RL 첫번째 포스팅에서 잠깐 소개했었던 CartPole문제를 고찰해보자.
Agent의 목표는 위 그림에 나오는 Cart를 화면 밖에 나가지 않으면서 동시에 위에 세워진 기둥을 쓰러트리지 않고 최대한 오래 버티는 것이 목표다. Environment의 $s$를 확인해보면 4차원의 벡터로 구성되어있고 각각의 차원이 의미하는 바는 1) Cart의 위치, 2)Cart의 속도, 3)기둥과 Cart와의 각도, 4)기둥의 각속도를 의미한다. 취할 수 있는 $\pi$는 왼쪽-오른쪽의 Binomial-distribution을 따른다. $\pi$는 지난 포스팅에서 Epsilon-greedy방식을 기반으로 한 Q-function업데이트로 변경되는 부분을 확인했으니 계산을 할 수 있는데, $s$의 정보가 연속적인 수치로 이루어짐을 생각하자. 앞선 코드의 일부
def set_qvalue(self,state,action,value):
if state not in self._qvalue: #초기화
self._qvalue[state] = {}
for possible_action in self.possible_actions:
self._qvalue[state][possible_actiosn]=0
else:
self._qvalue[state][action]=value
와 같이 Q-function을 테이블 형태로 만들기가 어려워진다. 이제 연속적인 환경에서의 agent가 $s$를 인식하는 부분에 대해서 논의하고 본격적인 CartPole문제를 해결해보도록 하자.
Agent designing for continous state
Modeling
CarPole같이 연속적인 $s$를 받고 $G_t$를 계산하는 agent는 일종의 함수와도 같은 존재로 생각할 수 있다. 구체적으로 이 agent는 학습 대상인 parameter, $\theta$로 이루어진 함수 $f$로 RL문제에선 다음과 같이 관계를 만들 수 있다.
\(f_{\theta}:s \rightarrow \mathbb{E\left(G_t\right)} .\)(1)
식 (1)처럼 만드는 모델, Neural network로 agent를 디자인 할 수 있다. 이제 Neural network는 $s$를 입력받아 $a$를 관여할 수 있는 $\pi$나 $Q(s,a)$를 출력받을 모델을 만들 수 있다. 전자를 출력하는 알고리즘은 후에 살펴볼 Actor-Critic방식이며, 후자를 출력하는 알고리즘은 Deep-Q-Network, (DQN)이다. 간단하게 torch로 해당 모델을 구현하면 다음과 같이 코딩할 수 있다.
class CartPole_DQN(nn.Module):
def __init__(self,input_dim=4,output_dim=2):
'''
입력인자
input_dim: 4, 의미 -> [위치, 속도, 각도, 각속도]
output_dim: 2, 의미 -> [Q(s,왼쪽), Q(s,오른쪽)]
'''
super(CartPole_DQN,self).__init__()
self.param1 = nn.Linear(input_dim,hidden_node1)
self.param2 = nn.Linear(hidden_node1,hidden_node2)
...
def forward(self,x):
x = F.relu(self.param1(x))
x = F.relu(self.param2(x))
...
return x = self.param_last(x)
### Objective function(Gradient Descent)
Neural network 모델로부터 Q-function혹은 Value-function을 구할 수 있게 되었다. Neural network의 꽃은 backpropagation을 통한 gradient descent를 시행하는 것이므로 모델링으로 부터 최적화의 단계로 이어지는 과정을 고려해보자. 지난 포스팅에서 RL의 목표인 TD error를 최소화 하는 과정이 우리가 흔히 아는 ML문제에서의 Cost function을 최소화 하는 부분과 동일한 맥락을 가진다. 이제 RL의 목적함수 ($J$)는 Neural network로 부터 얻은 Value-function(Q-function)을 참 Value-function(Q-function)으로 맞추도록 Squared-error로 설정하면 된다.
-
Value objective function \(J_{\theta}(s) = \left\{ V_{\pi}(s) - V_{\theta}(s) \right\}^2.\)(2)
-
Q objective function \(J_{\theta}(s) = \left\{ Q_{\pi}(s,a) - Q_{\theta}(s,a) \right\}^2.\)(3)
식 (2),(3)의 아래첨자 $\theta$는 Neural network모델을, $\pi$는 최적 $a$ 확률분포 정책이다. 각각의 식을 TD형태로 바꾸고 $\theta$에 대한 미분으로 풀어쓰면 다음과 같이 변형된다.
-
Value-function update term \(\nabla_{\theta}J_{\theta}(s)=-\alpha \left\{R+\gamma V_{\pi}(s') - V_{\theta}(s) \right\}\nabla_{\theta}V_{\theta}(s).\)(4)
-
Q-function update term \(\nabla_{\theta}J_{\theta}(s)=-\alpha \left\{R+\gamma Q_{\pi}(s',a) - Q_{\theta}(s,a) \right\}\nabla_{\theta}Q_{\theta}(s,a).\)(5)
이번 포스팅은 가볍게 넘어가는 의미로 이 정도 까지 이론 부분을 요약하고 CartPole문제를 Neural network로 풀어보는 예제를 살펴보겠다.
Pytorch CartPole tutorial
문제에 대한 상황은 앞에서도 언급했으니 각설하고 RL 해법에 대해서 집중하도록 하자. 지금까지 살펴본 RL풀이 전략인 SARSA와 Off-policy Q-learning의 Q-function을 Neural network모델로 뽑아보는 구조까지만 살펴보는것에 주목하면 된다. 전체 코드는 링크를 통해서 확인하기 바란다.
중요한 코드블럭 순서대로 코드를 리뷰하자. 첫째로 중요 라이브러리 호출 부분과 CarPole 문제 환경변경에 대한 코드블럭이다.
import gym
import numpy as np
import torch
import torch.optim as optim
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import copy
import random
env = gym.make('CartPole-v1')
env._max_episode_steps=1000 # 기본 CarPole의 최대 maximum step은 500으로 고정 -> 필자는 1000으로 customizing
print(env._max_episode_steps)
기본 CartPole은 500step을 버티면 문제를 풀었다고 가정하는데, 필자는 이 부분이 굉장히 짧다고 느꼈다. 따라서 env._max_episode_steps를 이용해 원하는 step만큼 조정을 한다. 이부분은 독자 여러분의 몫으로 남겨두도록 하겠다.
다음, Neural network모델 디자인 부분이다. Pytorch의 Neural network모델을 만드는 기본 방식을 덧붙여 구체적인 action을 선택할수 있도록 get_action이란 내부 method를 하나 디자인 해주었다.
class NN_model(nn.Module):
def __init__(self,input_dim=n_state,output_dim=n_action):
super(NN_model,self).__init__()
'''
입력변수
input_dim: state의 차원 -> cartpole [위치, 속도, 각도, 각속도]
output_dim: action의 차원 -> cartpole [왼쪽, 오른쪽]
N.N 구조
4 layer구조 (2 hidden layer).
hidden node개수는 64개로 통일.
activation function은 Relu 설정
'''
self.lin1 = nn.Linear(input_dim,64)
self.lin2 = nn.Linear(64,64)
self.lin3 = nn.Linear(64,output_dim)
def forward(self,x):
x = F.relu(self.lin1(x))
x = F.relu(self.lin2(x))
x = self.lin3(x)
return x
#def get_action(self,x,epsilon):
# 추후 설명 계속
class 구문처럼 1-hidden layer, 3_layer구조의 activation_function으로 ReLU함수를 이용하였다. 마지막 layer에서는 Q-function의 값을 제약걸면 안되므로 activation function을 넣지 않는다.
RL구조 함수블록은 다음과 같이 작성한다.
# 아직 이 블럭코드는 실행하면 안됨! 구조만 짜놓기
def play_or_train_agent(env,agent,eps,train=True):
'''
목표: agent를 환경에 맞게 train할것인지 단순 play할것인지 구성
입력인자
env: environment(CartPole)
agent: agnet
eps: epsilon-greedy (초기: 1, 최종: 0.1밑으론 하락x)
train: 학습여부(True: 학습, False: play)
출력인자
total_reward:
loss: 모니터링을 위한 TD error의 추이
'''
s = env.reset()
total_reward = 0
for t in range(env._max_episode_steps):
#<! s로 부터 action추출>
next_s,reward,done,_ = env.step(action)
total_reward += reward
if train:
#<! TD loss계산 및 업데이트>
s = next_s
if done:
break
return total_reward, loss
위 코드블럭은 환경을 새롭게 세팅하고 gym에 맞도록 action을 수행하는 과정은 모두 동일하다. 우리가 신경써야할 부분은 1) 주석처리된 N.N 모델로부터 $a$를 추출하고, 2) TD loss를 minimize시켜 agent를 학습시키는 두 부분만 구현해주면 된다.
$a$를 추출하는 단계는 우리가 앞서 구현한 Neural network 모델 클래스 내부에 작성하지 않았던 get_action method를 이용해서 구현해준다. 아래 코드블럭을 모델 클래스 하부에 붙여서 사용하게 된다.
def get_action(self,state,epsilon=0):
'''
목적: state로 부터 action추출
입력인자
state: 상태 -> shape[None,4]
epsilon: epsilon, -> scalar
출력인자
action: gym integer [0 or 1] -> Cartpole
'''
x = torch.FloatTensor(state)
Q_value = self.forward(x).detach().cpu().numpy()
if np.random.uniform(0,1) < epsilon:
action = np.argmax(np.random.uniform(0,1,size=Q_value.shape))
else:
action = np.argmax(Q_value)
return int(action)
위 코드 블럭은 설명을 덧붙이겠다. 입력인자 x가 모델을 통과해서 Q-function값을 환산한다. 중간에 임의의 $0~1$
사이의 확률변수 p를 이용해 epsilon-greedy를 적용한다. 확률 변수(p)가 epsilon값보다 작으면 취하는 action은 Q-function의 값 중 최대값을 환산하는 ‘Index’를 출력하는 np.argmax로 얻어진다. 그렇지 않은 경우 임의로 $a$에 해당하는 ‘Index’를 출력한다. 참고로 gym carpole문제의 action의 의미는 다음과 같다.
- Action meaning
- Left moving : 0
- Right moving : 1
다음 TD loss를 계산하는 구문은 다음과 같다.
def TD_loss(state,action,reward,next_state,done,gamma=0.99,agent=agent):
'''
목적: TD loss계산후 agent 학습
목적함수: (Reward+gammma*max_a{Q(s',a)} - Q(s,a))**2
입력인자
state: 상태
action: 액션
reward: 보상
next_state: 다음상태
done: 종료여부
gamma: discount factor(할인율)
agent: agent
출력인자
td_loss: 모니터링을 위한 TD error의 추이
'''
state = torch.FloatTensor(state)
action = torch.LongTensor(action)
reward = torch.FloatTensor(reward)
next_state = torch.FloatTensor(next_state)
done = torch.tensor(done,dtype=torch.uint8)
Q_current = agent(state)
Q_current = Q_current[range(state.shape[0]),action]
Q_next = agent(next_state)
Value_next = torch.max(Q_next,dim=1).values
target_value = reward+gamma*Value_next
target_value = torch.where(done,reward,target_value)
td_loss = torch.mean((Q_current-target_value.detach())**2)
return td_loss
입력변수 처리부분은 코드가 길어지고 지저분해서 과감히 생략했음을 밝힌다. TD loss를 구하고 업데이트 하는 과정은 Off-policy q-learning방식을 이용했다. Q_current변수항목을 통해 우리가 알고자 하는 특정 $s,a$의 Q-function값을 구하고 Value_next변수를 통해 $max_{a’}Q(s’,a’)$를 적용했음을 확인하라.
target_value는 에피소드가 종료되는 시점에 따라 변하는데 에피소드 종료시 $s’$라는 것은 존재하지 않으므로 $target=R$이 되고, 그렇지 않을때는 $R+\gamma \max_{a’}Q(s’,a’)$를 target으로 삼아 학습을 진행한다.
[주의]한 가지, 코딩상에서 언급해야 할 부분이 td_loss에서 target_value.detach()옵션이 있는데 이 이유는 detach를 통해서 Neural network모델의 gradient graph를 해제시키지 않으면 target_value자체도 업데이트를 하게 된다. 실제로 target_value은 업데이트 하지 않는 대상이고, agent모델이 업데이트를 하므로 이를 분리하기 위해 신경써야한다.
이제 종합해서 완성시키지 못했던 코드블럭을 완성시켜서 학습을 진행시켜보자.
# 이제 코드 블럭을 완성합시다
def play_or_train_agent(env,agent,optimizer,eps,train=False):
'''
목표: agent를 환경에 맞게 train할것인지 단순 play할것인지 구성
입력인자
env: environment(CartPole)
agent: agnet
optimizer: optimizer
eps: epsilon-greedy (초기: 1, 최종: 0.2밑으론 하락x)
train: 학습여부(True: 학습, False: play)
출력인자
total_reward: 최종보상
loss: 모니터링을 위한 TD error의 추이
'''
total_reward = 0
s = env.reset()
while True:
action = agent.get_action([s],epsilon=eps)
new_s, reward, done, _ = env.step(action)
total_reward += reward
if train:
optimizer.zero_grad()
loss = TD_loss([s],[action],[reward],[new_s],[done],agent=agent)
loss.backward()
optimizer.step()
s = new_s
if done:
break
if train:
return total_reward, loss
else:
return None
# 주 학습 - 에피소드마다 reward, td_loss값의 추이를 지켜봅시다
from tqdm import trange
from IPython.display import clear_output
agent = NN_model()
optimizer = optim.Adam(agent.parameters(),lr=1e-04)
episode_rewards, TD_losses = [], []
max_episodes = 100
mini_sessions = 50
eps = 0.5
for episode in trange(max_episodes):
mini_reward, mini_td = [], []
for mini_session in range(mini_sessions):
episode_reward, td_loss = play_or_train_agent(env,agent=agent,optimizer=optimizer,eps=eps,train=True)
mini_reward.append(episode_reward)
mini_td.append(td_loss.item())
eps *= 0.99
if eps < 1e-04:
eps=0.1
episode_rewards.append(np.mean(mini_reward))
TD_losses.append(np.mean(mini_td))
clear_output(True)
print("Episode",episode)
print("Epsilon",eps)
plt.figure(figsize=[12, 10])
plt.subplot(2,1,1)
plt.title("Total reward per each episode")
plt.plot(episode_rewards)
plt.grid()
plt.subplot(2,1,2)
plt.title("Td loss trend per each episode")
plt.plot(TD_losses)
plt.grid()
plt.show()
if np.mean(mini_reward) >= 500:
print(f"Agent finds solution! Final score : {np.mean(mini_reward)}")
break
위 코드를 매 에피소드 마다의 total_reward와 TD_loss로 그래프를 그리면 다음과 같은 결과가 나타난다.
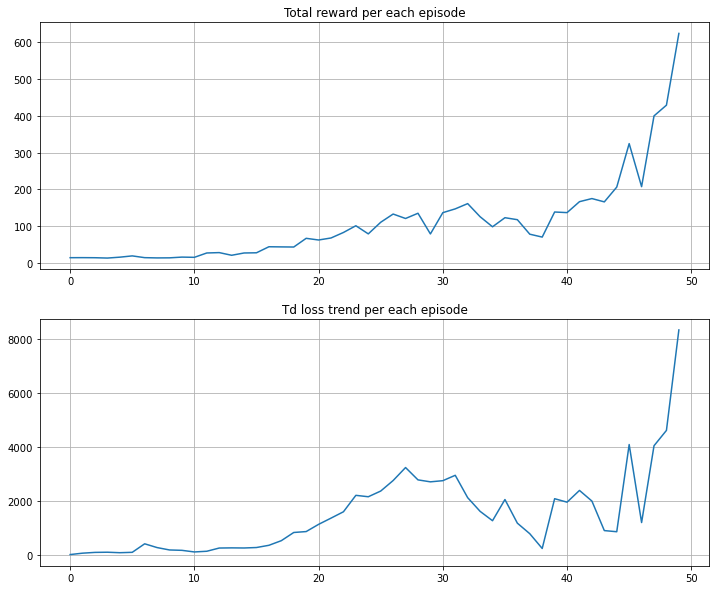
필자는 매 50회의 반복 세션의 평균 Reward가 500이상이라고 판단하면 충분히 agent가 solution을 구했다고 파악하고 계산을 종료하였다. 위 코드의 break구문을 사용하지 않으면 상당히 오랜시간동안 계산을 수행하니 주의하기 바란다.
지금까지 간략하게 Neural network를 통해서 연속적인 $s$에서의 agent가 Value-function, Q-function을 업데이트 시키는 알고리즘에 대해서 살펴보았다. 이제 다음 포스팅에서 한 단계 발전된 알고리즘, DQN을 리뷰해보고 CartPole보다 더 재미있는 예제를 살펴보도록하겠다.