Bellman equation을 통해서 agent의 최종 보상의 개념을 공부하였다. 이 부분이 익숙하지 않다면 반드시 복습하고 포스트를 봐주기 바란다. 지금까지 우리는 최종보상, $G_t$를 구하는 과정으로 동적계획법(Dynamic Programming, DP)로 해결했고 튜토리얼은 $\pi$가 고정적인 상황에서만 문제를 다루었다. 이제 다음 단계로 agent가 그렇게 계산된 Value-function 혹은 Q-function을 이용해서 $\pi$를 구체적으로 업데이트 시키는 과정에 대해서 살펴보고자 한다.
Policy update
$\pi$가 $s$에 대해서 최적의 action을 주도록 update하는 과정은 큰 관점으로 보았을때 매우 간단하다.
- $\pi$가 최대 Value-function을 주는 $a$ probability에 적합 여부를 평가를 한다.
- 평가시 부적합하다면 $\pi$를 최대 Value-function을 주도록 반복한다
각 단계 하나하나를 심층있게 살펴보자
Policy evaluation
현재 취하고 있는 $\pi$가 최적의 policy인지 아직은 모른다. 따라서 업데이트를 계속해나가는 것이다.
\(V_1 \rightarrow V_2 \cdots \rightarrow V_{\pi}.\)(1)
Value_function의 아래첨자는 몇회 반복했는지의 iteration을 나타낸다. 일반화를 시키면 k차시의 $\pi$를 평가하기 위한 Value_function의 수식은 다음과 같다.
\(V_{k+1}(s) = \sum_{a \in \mathcal{A}}{\pi (a \vert s)} \left\{R_{s}^{a}+\gamma \sum_{s' \in \mathcal{S}} P_{ss'}^{a} V_{k}(s')\right\}.\)(2)
Policy iteration
k차시마다 얻은 $V_k$가 식 (2)을 통해서 얻어졌다면, 다음 차시의 $\pi$는 탐욕(greedy)방식으로 획득한다.
\(\pi'=greedy(V_{\pi}).\)(3)
이제 Policy evaluation과 Policy iteration의 관계를 그림으로 나타내면 다음과 같다(David silver 교수님 강의자료 첨부)
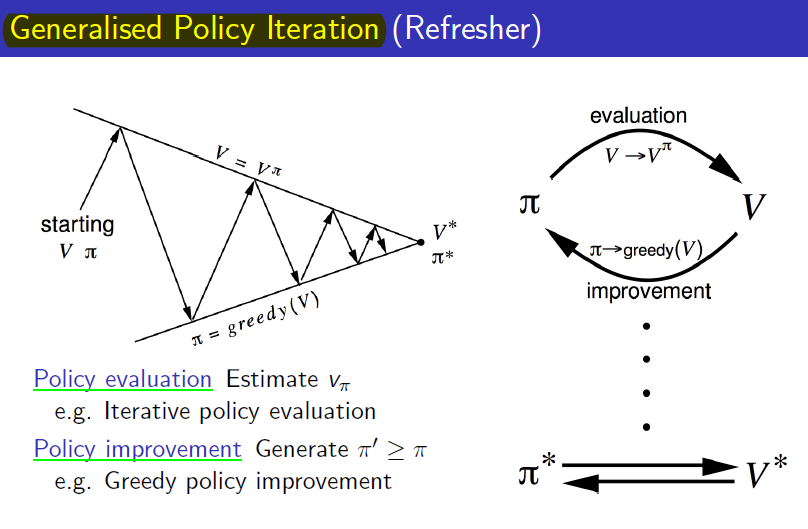
Monte-Carlo prediction & Temporal Difference prediction
Value-function 수식, ($V(s)=\mathbb{E}[G_t \vert s_t=s]$)에선 기대값이라는 개념이 있다. 정확한 Value-function에 대해 알아야 한다면 $P_{ss’}^{a}$에 대한 모든 경우에 대해 올바르게 계산해야하고 어마어마한 계산량을 처리해야하는 문제에 직면하게된다. 이는 실질적인 RL의 문제가 아니라, 앞서도 언급한 모든 environment의 속성을 완벽하게 파악하고 고려하는 Model based 방식으로 비 현실적인 상황에서의 문제를 해결하는 방식이다. 우리가 알고싶은 RL의 agent는 이와 같은 이상적인 Model base 방식이 아닌, Model free상황에서도 문제를 해결해야한다. 위 Policy iteration을 하는 과정을 현실적으로 바라보는 관점인 Monete-Carlo방식과 Temporal Difference방식을 차례차례 살펴보자.
Monte-Carlo prediction
혹시 Monte-Carlo 방식에 대해서 처음 들어보았다면 이 링크중 “Monte-Carlo”방식에 대한 설명을 참고하라. MC방식을 이용하면 기대값을 적정수의 반복을 가지고 샘플링으로 어림추산을 하는 방식으로 소위 ‘퉁’쳐서 계산한다.
\(\begin{align} V_{\pi}(s) &= \mathbb{E}{\pi}[G_t\vert s_t=s] \\ &= \mathbb{E}{\pi}[R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \vert s_t=s] \\ &= \mathbb{E}{\pi}[R_{t+1}+\gamma \left( {R_{t+2}}+\gamma{R_{t+3}}\cdots \right) \vert s_t=s] \\ &= \mathbb{E}{\pi}[R_{t+1}+\gamma G_{t+1} \vert s_t=s] \\ &= \mathbb{E}{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1}) \vert s_t=s] \end{align}.\)(4)
식 (4)의 기대값 부분을 (지금 단계에선 $a$를 구체적으로 생각하지 말고) 샘플링을 통해서 agent가 더 이상 $a$를 취할 수 없는 종료시점$(M)$까지 도달했다고 가정해보자.
\(\begin{align} V_{M}(s) &\approx \frac{1}{M} {\sum_{i=1}^{M}{G_i}} \\ &\approx \frac{1}{M} \left( G_M + {\sum_{i=1}^{M-1}{G_i}} \right) \\ &\approx \frac{1}{M} \left \{ G_M + (M-1)V_{M-1}(s) \right \} \\ &\approx V_{M-1}(s) + \frac{1}{M} \left \{ G_{M}-V_{M-1}(s) \right \} \end{align}.\)(5)
식 (5)가 도달되는 과정을 그림으로 표현하면 다음과 같다.

그림을 통해서 Value-function과 Q-function간의 관계를 유심히 살펴보면 $G_t$가 종료되는 시점(네모 사각형)이 분명히 존재하지만 매 차시의 $a$이 “임의로 선택”된다. 여기서 “임의로 선택”된다는 점이 상당히 꺼림직하다. 그 이유는 1) Value-function을 구하는 과정에서 Model-based방식이 필요와 2) Value-function의 부재로 인한 Policy iteration이 매끄럽지 못하다는 점이다. 여기서 잠시만 Bellman optimality equation에서 Optimal policy, $\pi_{*}$를 구하는 수식을 복기해보자.
\(\pi_{*}(a \vert s) = \text{argmax}_{a \in \mathcal{A}} \left\{ R_{s}^{a} + \gamma \sum_{s' in S} P_{ss'}^{a}V(s') \right\} .\)(6)
식 (6)의 state transition probability, $P_{ss’}^{a}$방식이 agent가 environment에 대한 모든 속성을 알고있다는 Model-based방식의 전제이다. 현실적으로 풀기위해 Model-free방식을 적용하기 위해 우리는 식 (6)의 $R.H.S$의 Value-function대신 Q-function을 대안으로 삼으면 된다.
\(\pi_{*}(a \vert s) = \text{argmax}_{a \in \mathcal{A}} Q(s,a) .\)(7)
식 (7)을 이용하면 더 이상 environment의 속성에 더이상 종속되지 않으며, 계산하기 어려웠던 Value-function을 직접적으로 계산하는 방식에서 벗어나게 된다. 다만, Q-function의 값도 정확히 아는 시점은 상황종료 시점인 $M$에서만 가능하며 그 시점까지 도달하는 동안은 $\pi$가 random action을 취해줘야 한다. 이 표현을 종합하여 $\pi$를 아래와 같이 정리하자.
\(\pi(a \vert .)= \begin{cases} \frac{\epsilon}{M}+1-\epsilon, & \text{if } a=\text{argmax}_{a \in \mathcal{A}}Q(s,a) \\ \frac{\epsilon}{M}, & \text{otherwise } . \end{cases} \\ \\ where, \epsilon = \text{Random action}\) (8)
$\epsilon$이라는 Random action방식이 처음 등장했다. 이렇게 환경에 대한 정보가 부족한 상황같은 특정조건에서 임의의 행동을 취하는 전략으로 Epsilon greedy방식이라고 하며 추후 여러번 나올 개념이므로 상세한 설명은 생략하겠다. 돌아와서 Q-function을 취할 수 있는 조건에서는 (Model-free인 조건으로 인해 random성질이 약간은 남아있지만) 최대 Q-function을 출력할 $a$를 선택하도록 하며, 그 이외의 조건에선 무조건 random action을 취한다는 방식이다. 조금 재미있게 표현하자면, 아무리 agent가 environment에 대해서 많이 학습을 한다고 해도 environment를 완벽하게 다 알지 않는 이상, 자신의 모르는 부분을 겸허히 받아들이고 자신의 사전지식을 내려 놓고 새로운 것을 받아들이려는 모습이라고 이해해주면 되겠다.
종합해서 평가하면 MC_prediction 방식으로 구한 근사 $G_t$결과의 특징은 High_variance & Low_bias특성을 가진다.
Temporal Difference prediction
Monte-Carlo 방식의 특성상 $G_t$를 구하는 과정에서 최종 state까지 Epsion greedy방식으로 랜덤하게 $a$를 취하는 상황을 보았다. MC방식은 DP방식과 비교할시 Model-free방식을 차용하고 있어 계산량의 측면에서 상대적으로 이점을 취하고 있으나 역시 최종 state까지 agent를 행동시켜야 하는 비합리적인 학습전략이다. 식 (4)의 Value-function을 합리적으로 계산할 수 있게끔 변화시킨 방식이 Temporal Difference(TD) 학습전략이다. 식 (4)를 변형시켜 합리적인 Value-function의 업데이트 관계식을 아래와 같이 표현해보자. $1/M$을 $\alpha$로 바꾸고, 흔히 아는 학습률 learning rate와 동치로 생각하면 된다.
\(\begin{align} V(s_t) &\leftarrow V(s_t) + \alpha \left \{ R_{t+1}+\gamma V(S_{t+1}) - V(s_t) \right \}\\ . \end{align}\) (9)

식 (9)처럼 Value-funcction의 업데이트 관계식을 표현할수 있는 이유는 DP관계식의 기대값을 샘플링 한 방식이기 때문이다. 이제 Value-function이 업데이트 하려는 목표(target)와 최소화 시켜야 하는 목적함수 Temporal Difference error, TD error는 식 (9)에서 표현하는 다음 항들이다.
- $Target: R_{t+1}+\gamma V(s_{t+1})$
- $TD \ error: R_{t+1}+\gamma V(s_{t+1}) - V(s_t)$

실질적으로 프로그래밍을 할때 TD-error 업데이트 과정이 매 순간마다 업데이트를 불 필요할 정도로 많이 수행하는데 부담이 있기에 Value function을 몇 스텝 뒤로 미루어 아래와 같이 계산을 할 수도 있다. 이 적정 스텝($n$)은 실용적인 부분이므로 문제를 해결하는 사람이 적절히 고려해서 풀어야할 부분이다.
\(V(s_t) \leftarrow V(s_t) + \alpha \left \{ R_{t+1}+\sum_{k=0}^{n-1}\gamma^{k} V(s_{t+k+1}) - V(s_t) \right \} .\) (10)
TD prediction방식의 특성을 곱씹어 보면 Value-function의 target이 현재로 부터 제한된 미래의 단계의 Value-function과의 관계이므로 Lower_variance & High_bias 특성을 가지게 된다. 언제나 ML문제는 Variance - Bias 간의 trade-off관계를 잘 조율해야하는데 MC방식과 비교하였을때 TD방식은 정 반대의 속성을 가지고 있다. 더군다나 식 (10)을 이용해서 식 (9)과 비교시 Variance를 높이고 Bias를 낮추는 기법을 사용할수 있으므로 현실적으로 RL의 문제를 풀때 해당 전략을 이용하게 된다. 한 가지 더 언급해야할 부분이 있는데, Value-function을 쓴다는 것은 MC 방법에서 언급한 것 처럼 environment의 model을 다 알고있다는 역설에 빠지게 된다. 따라서 이 역설을 해결하기 위해 environment model을 벗어나기 위한 방식으로 식 (9)을 Q-function으로 바꾸어 준다.
\(Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) + \alpha \left \{ R_{t+1}+\gamma Q(s_{t+1},a_{t+1}) - Q(s_{t},a_{t}) \right \} .\) (11)
TD prediction - SARSA vs Off-policy Q-learning
식 (11)로부터 파생되는 구체적인 TD방식을 근거로한 알고리즘들을 살펴보겠다.
SARSA
식 (11)까지 Q-function에 도달하는 과정의 알고리즘 단계를 살펴보자.
- 모든 $s,a$에 대해 Q-function을 초기화 한다.
- Epsilon-greedy 방식을 도입해 $a$를 취한다.
- $a$로부터 $s’, R$을 관찰한다.
- Epsilon-greedy 방식을 도입해 $s’$로 부터 $a’$를 취한다.
- Q-업데이트, $Q(s,a)\leftarrow{Q(s,a)}+\alpha\left{R+\gamma{Q(s’,a’)}-Q(s,a)\right}$
- $s \leftarrow s’$, $a \leftarrow a’$ 로 업데이트
- Step 3-6까지 반복
눈치가 빠른 독자라면 SARSA의 이름이 알고리즘의 5번째 단계에서 업데이트하는 대상 Q의 $s,a,R,s’,a’$를 따왔음을 확인할 수 있다. SARSA방식은 $s’$에서의 $a’$을 취할때 Epsilon-greedy방식을 취하는데 이는 탐험해보지 못한 상태에서의 행동양식을 agent가 가진 사전지식(Q-function)을 이용하는 것에만 그치지 않고 임의의 행동을 취해주어 agent가 생각해보지 못했던 일종의 새로운 ‘시도’를 취하게끔 유도한다. 임의의 행동을 시도한다는 말은 RL에서 Exploration을 적용했다고 표현하는데 SARSA방식은 이런 action에 대해서 모르고 있는 상황에서도 물론, 자신이 알고있다는 사전지식에도 Model-free속성으로 인한 결함이 있음을 인정해 새로운 시도를 취하는 학습방식이다. 덧붙여 매번 $a$를 Epsilon-greedy방식을 적용한 $\pi$로부터 획득하므로 SARSA는 On-policy 학습법이라고 말하니 참고하기 바란다.
Off-policy Q-learning
SARSA의 알고리즘처럼 우선 Off-policy Q-learning의 알고리즘 단계를 살펴보자.
- 모든 $s,a$에 대해 Q-function을 초기화 한다.
- Epsilon-greedy 방식을 도입해 $a$를 취하고, $a$로부터 $s’, R$을 관찰한다.
- Q-업데이트, $Q(s,a)\leftarrow{Q(s,a)}+\alpha\left{R+\gamma\text{max}_{a}Q(s’,a)-Q(s,a)\right}$
- $s \leftarrow s’$로 업데이트
- Step 2-4까지 반복
SARSA와의 차이점으로 TD target부분을 주목하면 되겠다. TD target의 Q-function을 선택할때 더 이상 Epsilon-greedy방식을 채용하지 않고 agent가 가지고 있는 Q-function안에서의 최선의 값을 선택함을 3번째 단계에서 살펴볼수 있다. 이렇게 $s’$에서의 Q-function을 구하는 과정에서 $\pi$가 적용되지 않는 학습방식을 Off-policy Q-learning 방식이라고 하며, 특징은 Exploration이 적용되지 않으므로 오로지 자기 자신의 선택만 옳다고 판단하는 부분이다.
이제 TD prediction으로 재미있는 문제를 살펴보도록하자.
Example: Cliff walking
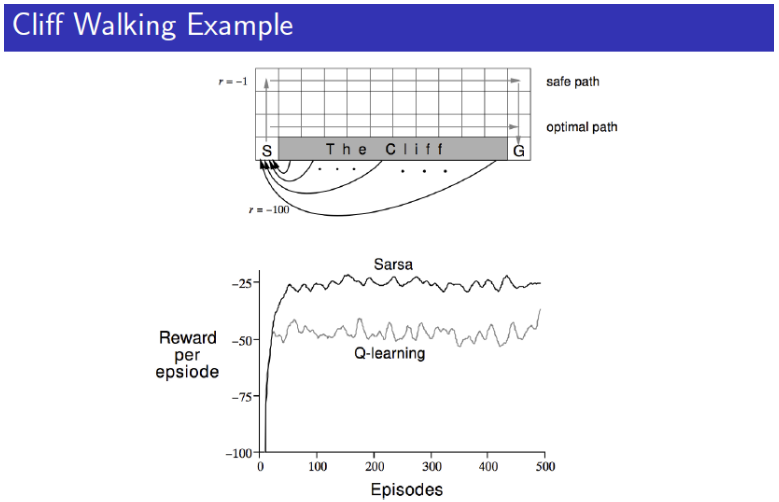
‘절벽 걷기’라는 재미있는 이름이 붙여진 문제는 역시 David silver교수님의 RL강의에서 나온 문제다. 위 그림처럼 agent가 이동을 개시하고 목표지점까지 최단경로로 이동하도록 학습하는 목표의 RL문제인데 ‘Cliff’라고 표현된 부분으로 이동하면 패널티를 받으며 에피소드가 종료된다. 이제 우리가 배운 TD prediction방식, SARSA와 Off policy Q-learning을 이용해서 agent를 최대한 빠르게 목표지점까지 도달 할 수 있도록 학습시켜보도록 하자.
문제 상황은 처음 RL포스팅에서 다룬 ‘gym’라이브러리 에서 구현이 되어있으니 이를 이용하면 된다. 참고로 필자는 예전에 처음 배웠을때 Cliff-walking을 손으로 다 환경을 구현하고 문제를 풀었는데 라이브러리가 있다는 사실에 다소 충격을 받았다…
import gym
import gym.envs.toy_text
env = gym.envs.toy_text.CliffWalkingEnv()
n_actions = env.action_space.n
print(env.__doc__) # 출력화면으로 대략적인 cliff walking 문제의 정보를 확인
gym의 구조에 맞게 대략 구조를 설계해보자
s = env.reset() # environment 초기화
total_reward = 0.
t_max = 10**4
for t in range(t_max): # 매 에피소드마다 무한정 반복할수 없으니 적정선에서 끊는다.
# <구현 필! SARSA, Q_learning agent에 맞게 action추출>
new_s, reward, done, _ = env.step(a) # agent의 action을 환경에 대입하고 s', R을 관찰
# <구현 필! SARSA, Q_learning agent학습 시행>
s = new_s # state swap
total_reward += r # 누중합
if done: # 목표에 도달했거나 절벽에 떨어졌다면 에피소드 종료
break
위 코드 블럭의 <구현 필!>이라고 표현한 부분만 우리가 구현하면 된다. SARSA방식과, Off policy Q-learning에 맞도록 action을 추출하고 Q-function을 업데이트 하는 학습을 각각 구현하는데 치중하자. 추가로 코드블럭에 t_max변수를 추가시켜서 무한정으로 하나의 에피소드에서 오랫동안 갇혀있는 상황을 방지하였다는 점을 인지하기 바란다.
다음 단계로 SARSA, Off-policy agent를 디자인하는 블록이다. get_value를 이용해 TD target삼는 부분에 유의하기 바란다. SARSA와 Off-policy방식의 결정적인 차이로 해당부분만 고려하면 된다. 먼저 SARSA agent이다. 코드블럭의 입력인자에 대한 주석을 음미하길 바란다.
class SARSA_agent():
def __init__(self,alpha=0.25,epsilon=0.2,gamma=0.99,possible_actions=range(n_actions)):
'''
class 입력인자
- alpha : 학습률 learning rate
- epsilon: epsilon, epsilon-greedy exploration
- gamma: 할인율, discount factor
- possible_actions: 선택할수있는 a의 옵션, cliff-walking: 'up,left,down,right'
SARSA agent 업데이트 알고리즘
- ***Epsilon-greedy*** 방식을 도입해 $a$를 취한다.
- $a$로부터 $s', R$을 관찰한다.
- ***Epsilon-greedy*** 방식을 도입해 $s'$로 부터 $a'$를 취한다.
- $Q(s,a) \leftarrow Q(s,a) + \alpha \left \{ R+\gamma Q(s',a') - Q(s,a) \right \}.$
- $s \leftarrow s'$, $a \leftarrow a'$ 로 업데이트
필수기능
- agent update(s,a,r,s') -> for update
- agent get_action(s) -> state로부터 action추출(Epsilon greedy)
부수기능
- agent get_qvalue(s, a) -> state, action으로 부터 Q_function값 추출
- agent get_values(s) -> state로부터 Value-function값 추출
'''
self.alpha = alpha
self.epsilon = epsilon
self.gamma = gamma
self.possible_actions=possible_actions
self._qvalue = {}
'----------------------------------------------------필수기능'
def update(self,state,action,reward,next_state):
# Q_update는 코딩상 다음과 같이 계산해준다
# Q(s,a) = (1-alpha)*Q(s,a)+alpha*(reward + gamma*V(s'))
# V(s')는 최적의 action-value Q(s',a')를 대용하기 때문
q_update = (1-self.alpha)*self.get_qvalue(state,action)+self.alpha*(reward+self.gamma*self.get_value(next_state))
self.set_qvalue(state,action,q_update)
def get_action(self,state):
'''
SARSA epsilon-greedy
'''
p = np.random.uniform(0,1)
if p<=self.epsilon:
best_action = random.choice(self.possible_actions)
else:
best_action = random.choice(self.possible_actions)
best_qvalue = self.get_qvalue(state,best_action)
for possible_action in self.possible_actions:
if self.get_qvalue(state,possible_action) >= best_qvalue:
best_action = possible_action
best_qvalue = self.get_qvalue(state,possible_action)
return best_action
'----------------------------------------------------부수기능'
def set_qvalue(self,state,action,value):
if state not in self._qvalue: #초기화
self._qvalue[state] = {}
for possible_action in self.possible_actions:
self._qvalue[state][possible_actiosn]=0
else:
self._qvalue[state][action]=value
def get_qvalue(self,state,action):
if state not in self._qvalue: #초기화
self._qvalue[state] = {}
for possible_action in self.possible_actions:
self._qvalue[state][possible_action] = 0
return self._qvalue[state][action]
def get_value(self,state):
'''
epsilon-greedy방식을 기반으로 Value값을 추산
SARSA
Q(s',a') ~ V(s')
policy
if action == argmaxQ(s,a)
policy[action] = eps/m + 1-eps
else
policy[action] = eps/m
Remind V(s) = sum_a { policy(a|s)*Q(s,a)}
'''
state_value = 0
policy = np.ones(len(self.possible_actions))*self.epsilon/len(self.possible_actions)
best_action = 0
max_val = self.get_qvalue(state,self.possible_actions[best_action])
for idx, possible_action in enumerate(self.possible_actions):
if max_val <= self.get_qvalue(state,possible_action):
best_action = idx
max_val = self.get_qvalue(state,possible_action)
policy[best_action] += 1-self.epsilon
for idx,possible_action in enumerate(self.possible_actions):
state_value += self.get_qvalue(state,possible_action)*policy[idx]
return state_value
다음은 Off-policy agent이다. 역시 주석부분을 음미하길 바란다.
class Off_Q_agent():
def __init__(self,alpha=0.25,epsilon=0.2,gamma=0.99,possible_actions=range(n_actions)):
'''
class 입력인자
- alpha : 학습률 learning rate
- epsilon: epsilon, epsilon-greedy exploration
- gamma: 할인율, discount factor
- possible_actions: 선택할수있는 a의 옵션, cliff-walking: 'up,left,down,right'
SARSA agent 업데이트 알고리즘
- ***Epsilon-greedy*** 방식을 도입해 $a$를 취한다.
- $a$로부터 $s', R$을 관찰한다.
- ***Epsilon-greedy*** 방식을 도입해 $s'$로 부터 $a'$를 취한다.
- $Q(s,a) \leftarrow Q(s,a) + \alpha \left \{ R+\gamma Q(s',a') - Q(s,a) \right \}.$
- $s \leftarrow s'$, $a \leftarrow a'$ 로 업데이트
필수기능
- agent update(s,a,r,s') -> for update
- agent get_action(s) -> state로부터 action추출(Epsilon greedy)
부수기능
- agent get_qvalue(s, a) -> state, action으로 부터 Q_function값 추출
- agent get_values(s) -> state로부터 Value-function값 추출
'''
self.alpha = alpha
self.epsilon = epsilon
self.gamma = gamma
self.possible_actions=possible_actions
self._qvalue = {}
'----------------------------------------------------필수기능'
def update(self,state,action,reward,next_state):
# Q_update는 코딩상 다음과 같이 계산해준다
# Q(s,a) = (1-alpha)*Q(s,a)+alpha*(reward + gamma*V(s'))
# 여기서 V(s')는 최적의 action-value Q(s',a')를 대용하기 때문에 이와 같이 치환
q_update = (1-self.alpha)*self.get_qvalue(state,action)+self.alpha*(reward+self.gamma*self.get_value(next_state))
self.set_qvalue(state,action,q_update)
def get_action(self,state):
'''
Off policy, epsilon-greedy
'''
p = np.random.uniform(0,1)
if p<=self.epsilon:
best_action = random.choice(self.possible_actions)
else:
best_action = random.choice(self.possible_actions)
best_qvalue = self.get_qvalue(state,best_action)
for possible_action in self.possible_actions:
if self.get_qvalue(state,possible_action) >= best_qvalue:
best_action = possible_action
best_qvalue = self.get_qvalue(state,possible_action)
return best_action
'----------------------------------------------------부수기능'
def set_qvalue(self,state,action,value):
if state not in self._qvalue: #초기화
self._qvalue[state] = {}
for possible_action in self.possible_actions:
self._qvalue[state][possible_actiosn]=0
else:
self._qvalue[state][action]=value
def get_qvalue(self,state,action):
if state not in self._qvalue: # 초기화
self._qvalue[state] = {}
for possible_action in self.possible_actions:
self._qvalue[state][possible_action] = 0
return self._qvalue[state][action]
def get_value(self,state):
'''
epsilon-greedy방식을 기반으로 Value값을 추산
Off-policy Q-learning -> no exploration
V(s) = max_a {Q(s,a)}
'''
state_value = []
for possible_action in self.possible_actions:
state_value.append(self.get_qvalue(state,possible_action))
state_value = max(state_value)
return state_value
각각의 agent는 $\epsilon, \gamma$값을 디폴트로 설정한 $0.2, 0.99$ 값으로 고정하고 가능한 $a$만 고려해준다. $a$인자는 정수형태로 입력되므로 range(env.action_space.n)로 “상,하,좌,우” 4가지 경우에 대해서 대응되게 세팅해준다
agent_SARSA = SARSA_agent(possible_actions=range(env.action_space.n))
agent_Q_learning = Off_Q_agent(possible_actions=range(env.action_space.n))
environment에 대해서 agent를 학습하는 단계, 위에서 미완성 시켰던 블록을 함수화 시켜준다. 함수는 최종보상값을 출력하도록 설계하자.
def agent_training(env,agent,t_max=10**4):
'''
입력인자
env : 환경 cliff-walking
agent: SARSA, Off-policy Q-learning agent
t_max: 인위적으로 에피소드 종료반복회차
'''
s = env.reset() # environment 초기화
total_reward = 0
for t in range(t_max):
a = agent.get_action(s) # <구현 필! SARSA, Q_learning agent에 맞게 action추출>
new_s, r, done, _ = env.step(a) # agent의 action을 환경에 대입하고 s', R을 관찰
agent.update(s,a,r,new_s) # <구현 필! SARSA, Q_learning agent학습 시행>
s = new_s
total_reward += r
if done:
break
return total_reward
아래 코드블럭을 이용해서 학습진행단계마다 agent가 어떻게 발전하는지 시각화 시켜보자.
from IPython.display import clear_output
import pandas as pd
def moving_average(x, span=100):
return pd.DataFrame({'x': np.asarray(x)}).x.ewm(span=span).mean().values
sarsa_rewards, off_q_rewards = [], []
for it in range(5000):
sarsa_rewards.append(agent_training(env,agent_SARSA))
off_q_rewards.append(agent_training(env,agent_Q_learning))
if it % 100 == 0:
clear_output(True)
print(f'Current iteration: {it}, process: {it/5000*100:.2f}%')
plt.title('SARS vs Off-policy')
plt.plot(moving_average(sarsa_rewards),label='SARSA')
plt.plot(moving_average(off_q_rewards),label='Off-policy')
plt.grid()
plt.legend()
plt.ylim(-500,0)
plt.show()
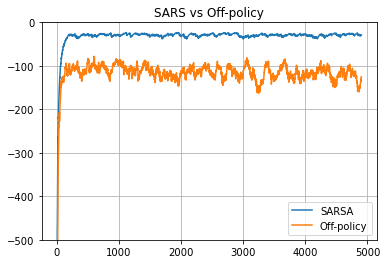
결과 그래프를 보면 제 아무리 agent가 환경에 대해서 학습을 했다고해도 자신이 모르고 있다는 부분을 인정하고 학습하는 Off-policy Q-learning 전략보다, On-policy SARSA 결과가 더 좋게 나옴을 확인 할 수 있었다.
혹시나 agent가 어떻게 거동하는지 보고 싶다면 아래 코드블럭을 이용해 시각화 할 수 있다.
def agent_playing(env,agent,t_max=10**4):
'''
입력인자
env : 환경 cliff-walking
agent: SARSA, Off-policy Q-learning agent
t_max: 인위적으로 에피소드 종료반복회차
'''
print('Cliff walking start!')
s = env.reset() # environment 초기화
total_reward = 0
print('')
for t in range(t_max):
print(f'Step {t:d}')
env.render()
a = agent.get_action(s) # <구현 필! SARSA, Q_learning agent에 맞게 action추출>
new_s, r, done, _ = env.step(a) # agent의 action을 환경에 대입하고 s', R을 관찰
s = new_s
total_reward += r
if done:
if s == 47:
print('Agent succeeded to solve the problem')
else:
print('Agent failed to solve the probelem')
break
agent_playing(env,agent_SARSA) # 혹은 agent_playing(env,agent_Q_learning)
해당 튜토리얼 코드 전 부분은 링크를 통해 확인해주기 바란다. 다음 포스팅에서는 테이블 형태의 $s$를 넘어서 연속적인 $s$에 대해서 어떻게 문제를 풀지 그 전략을 살펴보겠다.