전통적인 머신러닝 기법으로 MCMC, Gaussian Process, 그리고 EM-method에 관해서 시간이 날때마다 정리해보고자 합니다. 한동안 뜸했는데 열심히 정리해보고 누군가에게 도움이 될만한 글이 되었으면 좋겠습니다. 그 첫번째 전통적인 머신러닝 기법의 방식으로 MCMC방법과 그 대표적인 예시인 Metropolis-Hasting 알고리즘을 살펴보겠습니다.

Monte Carlo

우리가 어떤 특별한 값, 예를들어 $\pi$라는 원주율 값을 구체적으로 알고싶다고 가정해봅시다. 원주율 $\pi$ 값을 대략 3.1415… 이렇게 외우는 값이 있는데 확실히 얼마! 이렇게 구하기가 굉장히 어렵습니다. 해석적으로 그 끝의 값을 알수없는 특별한 숫자이기도 하고, 그런데 최대한 정확히 알기는 알아야 하는 신비한 숫자 어떻게 구할 수 있을까요?

정확히 구할수 없으면, 근사를 해서 구하는 대안책을 세우는 방법이 있습니다. 아래 그림을 살펴보겠습니다!

${0}\leq {x} \leq {1}$, $ {0}\leq {y} \leq {1}$ 영역에서 사분원 공간을 잡아넣고 임의로 점을 확 산개시켜버린다고 가정해봅시다.

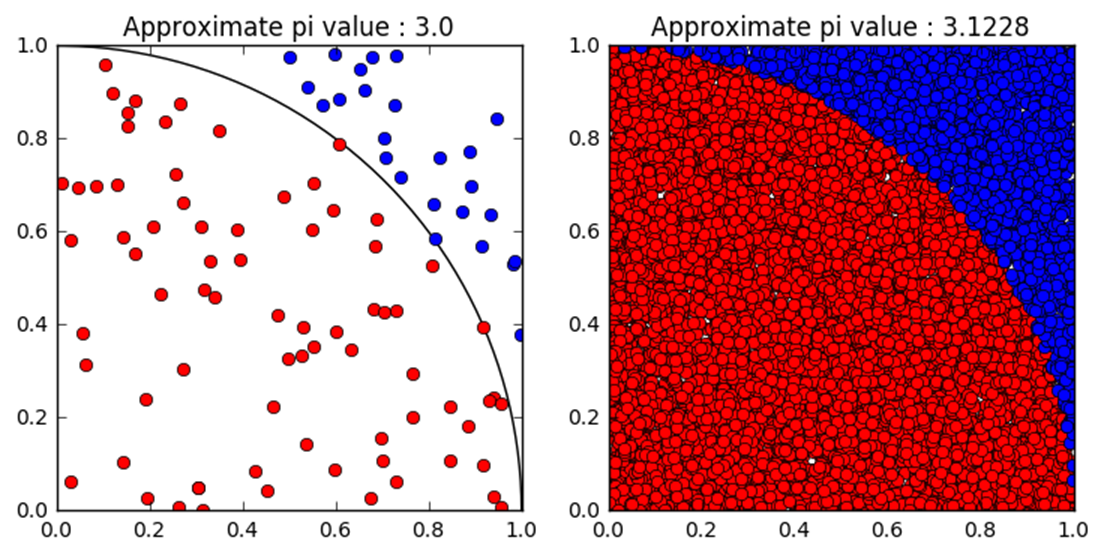
우리가 산개시켜버린 점의 개수($N_{total}$)를 알고, 사분원 공간안에 있는 점의 개수($N_{red}$), 그리고 사분원 공간 바깥에 있는 점의 개수($N_{blue}$)를 잘조합시키면 아래 근사 관계식이 만들어집니다.

\(\frac{\pi}{4} \approx \frac{N_{red}}{N_{total}}\).(1)

\(P(\theta) = \frac{N_{red}}{N_{total}}\).(2)

식 1번의 L.H.S는 단위 사분면의 면적과 동일합니다. 반면, R.H.S는 균일하게 뿌린 점중에서 사분면 안에 들어온 점의 비율입니다. 여기서, 점들을 적게 뿌린다면 식 1번의 수식의 근사의 정확도는 표본의 수가 적기때문에 신뢰도가 높지 않게됩니다. 100개의 점으로 샘플링을 해보면 $\pi \approx 3.0$ 정도로 계산되지만, 10000개의 점으로 샘플링을 하면 $\pi \approx 3.1228$로 결과를 구합니다. 이렇게 특정한 값을 구하는데 샘플링 확률 $P(\theta)$을 이용하여 근사식을 이용하는 방식을 일컬어 Monte Carlo method라고 부릅니다.

Markov Chain

MCMC중 첫번째 MC가 Monte Carlo라는 말을 알았으니 두번째 MC가 무슨 말인지 알아볼 차례입니다. 용어부터 말하자면 Markov Chain인데, 정의를 위키백과에서 복사-붙여넣기 해보면

“확률론에서 마르코프 연쇄는 이산 시간 확률 과정이다. 마르코프 연쇄는 시간에 따른 계의 상태의 변화를 나타낸다.”

이 개념 역시, 예제와 함께 살펴보도록 합시다.

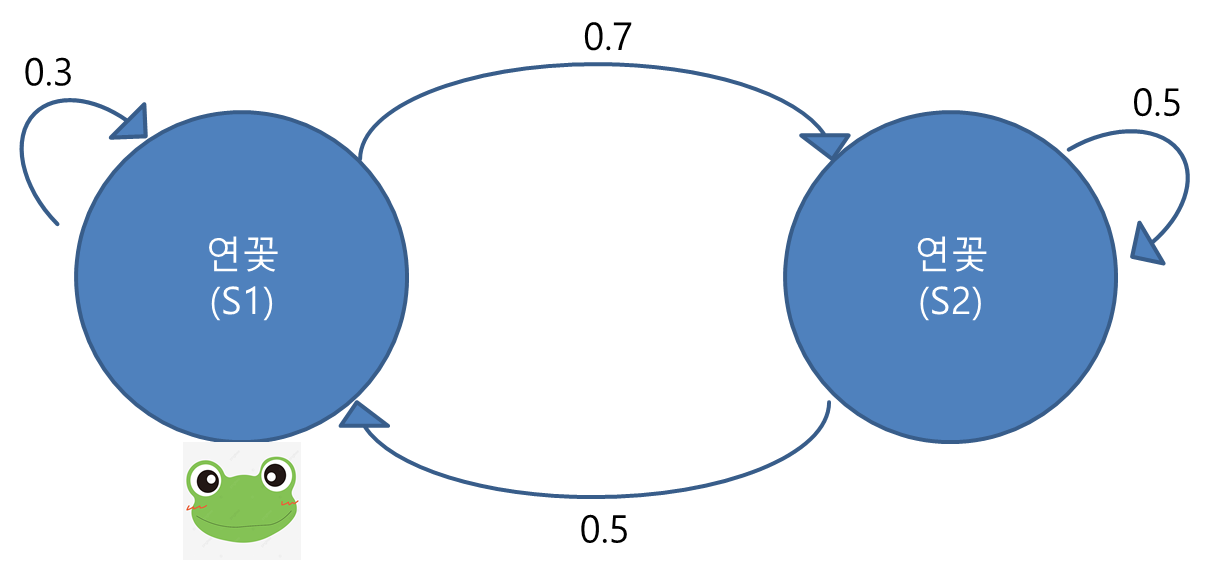
(필자의 엉성한 실력으로 만든 그림이지만 이쁘게 봐주길 바랍니다^^;;)연못에 연꽃이 두개가 있고, 그 안에 개구리가 있는 상황입니다.

개구리는 한번에 폴짝폴짝 뛰어다니며 연꽃을 이동하거나 가만히 있거나 하는 행동을 합니다. 개구리가 그림같은 확률로 움직인다면 매우 많은 $n$차시를 관찰하면, 개구리는 각각의 연꽃에 어느 확률 - $P(S_1),P(S_2)$ -로 있을 것인지 구해보는 것이 문제의 목표입니다. 개구리는 차시마다 한번씩 움직이므로 시계열 관계로 행동을 취하고, 연꽃이라는 시스템 안에서 그림과 같은 거동사슬(chain)으로 지배당하는 것을 인지하기 바랍니다.

초기 차시에 개구리가 $S_1$에 있다고 하면 첫번째, 두번째, 그리고 $n$ 차시에서의 연꽃 이산확률분포는 각각 다음표로 계산이 가능합니다.

차시	$P(S_1)$	$P(S_2)$
0	$1$	$0$
1	$0.3=1 \times 0.3+0 \times 0.5$	$0.7=1 \times 0.7+0 \times 0.5$
2	$0.44=0.3 \times 0.3+0.7 \times 0.5$	$0.56=0.3 \times 0.7+0.7 \times 0.5$
$\vdots$	$\vdots$	$\vdots$
n	${P_{n-1}(S_1)}\times{0.3}+{P_{n-1}(S_2)}\times{0.5} \approx {0.48}$	${P_{n-1}(S_1)}\times{0.7}+{P_{n-1}(S_2)}\times{0.5}\approx{0.52}$

• 초기단계 $\rightarrow$ 1차시
  • 초기 개구리의 위치는 $S_1$에 확정적으로 있으므로 1차시에 자기자신으로 있을 확률 30%, $S_2$로 이동할 확률 70%는 쉽게 생각 할 수 있습니다. 여기서 대부분 한가지 계산을 간과하기 쉬운데, 초기 개구리 위치가 $S_2$에 없다고 해서 $S_2$에서 유입되는 이동에 대해서 무시하는 부분입니다. 하지만 엄연히 위 테이블처럼 1차시에서 $S_2$에서 유입이 되거나 자기자리에 있는 $0$의 확률을 엄연히 계산해줘야한다.
• 1차시 $\rightarrow$ 2차시
  • 개구리가 1번 뛰었습니다. $S_1, S_2$에 있을 확률이 30%, 70%로 각각 계산되는 것을 확인했습니다. 이제 2차시에 대해서 계산해봅시다.
    • 첫번째 연꽃에 있을 확률은 “이전 차시의 $S_1$에서 가만히 있을 확률 + 이전 차시의 $S_2$에서 유입될 확률 44%,”
    • 두번째 연꽃에 있을 확률은 “이전 차시의 $S_1$에서 유입될 확률 + 이전 차시의 $S_2$에서 가만히 있을 확률 56%,”
• n차시 이제는 점화식으로 표현이 가능합니다. 1차시에서 2차시로 가는 것처럼, 다음 차시에서의 연꽃마다의 개구리가 있을 확률은 다른 요인보다 ‘이전차시에서의 확률분포’가 중요하다는 사실을 인지하면 됩니다. 최종적으로 $n$차시를 거의 무한대로 확장하면 확률 값은 연꽃 순서대로 48%, 52%로 수렴합니다.

점화식을 썼으니 포스팅을 본 독자들도 이 예시대로 몇 번 계산하면 검증이 가능할것으로 믿습니다. 시간나면 직접 계산해보기를 적극 추천드립니다. 이렇게 데이터의 샘플링하는 과정이 시계열처럼 지배가 되어있고, 확률분포의 변수(i.e 연꽃)가 서로서로 사슬처럼 엮여있는 확률 과정 전반을 Markov Chain이라고 부릅니다.

Monete Carlo + Markov Chain = MCMC

즉, 어떤 확률값을 알고 싶을때 직접적으로 구하기 어려우니 매우 많은 수행과정 + 확률변수가 Markov chain으로 지배당할때 그 방식을 구하는 법을 MCMC라고 합니다.

Metropolis-Hasting algorithm

MCMC라는 개념을 이해했으니 나머지 한 단계 더 나아가서 구체적인 확률분포의 샘플링 방식을 구체적으로 살펴보겠습니다. MCMC의 대표적인 샘플링 방식인 Metropolis-Hasting(MH) 방식을 보겠습니다.

우리는 위 개구리 예시에서 아주 운좋게도(!) 개구리가 연꽃과 연꽃간의 이동하거나 가만히 있을 확률, 상태변화 확률($T$)에 대한 정보를 명확하게 알고 있었습니다. 그래서 우리는 개구리가 구체적인 확률로 어느 연꽃에 있을것인지 계산 가능했지만 이것은 아주 이상적인 상황입니다. 그러나 실제 사람이나 인공지능이 마주하게 될 문제는 개구리가 연꽃을 구체적으로 이동할 $T$에 대한 정보를 얻을 수가 없습니다. 그렇다고 포기할 수는 없는 법이므로 대안책을 내세운것이 바로 Metro-Hasting sampling방식입니다.

MH방식을 바로 설명하기 이전에 개념을 쉽게 알기 위해 선행지식인 Detailed balance의 개념을 알아야 합니다.

\(P(S_1)T({S_1}\rightarrow{S_2})=P(S_2)T({S_2}\rightarrow{S_1})\).(3)

식 3에서 우리는 이상적인 상황에서만 $T$에 대한 정보를 모두 가지고 있지만, 그렇지 못한 현실에서의 $T$를 다음과 같이 분리해서 생각해보겠습니다.

\(T({x}\rightarrow{y}) = Q({x}\rightarrow{y})A({x}\rightarrow{y})\).(4)

식 4의 L.H.S는 우리가 이상적으로 알고 싶은 상태변화 확률, R.H.S의 $Q$는 $x\rightarrow{y}$로 이동할지 말지 제안하는 임의의 제안함수(proposal distribution), $A$는 $x\rightarrow{y}$가 합당한지 평가하는 지표 Critic입니다. 노파심에 덧붙이자면 Proposal distribution은 ‘다음 위치로 탐험할지 안할지’ 말 그대로 제안하는 확률분포 입니다. 즉, 사용자가 Gaussian distribution, Beta distribution, Gamma distribution등 다양한 확률분포가 여기에 대입 시킬 수 있습니다. 이제, 식 4를 식 3에 대입하여 식을 변형시킬수 있습니다. 그 변형시킬 식의 목표는 $x\rightarrow{y}$가 Detailed balance를 통해 합당한지 평가하는 Acceptance($\alpha$)입니다.

\(\alpha=\frac{A(x{\rightarrow}y)}{A(y{\rightarrow}x)}=\frac{P(y)Q(y{\rightarrow}x)}{P(x)Q(x{\rightarrow}y)}\).(5)

• Case 1: $\alpha \geq 1$
  • Acceptance가 1보다 큽니다. 이는 식 5의 중간변을에서 변수가 이동하는 방향이 $x\rightarrow{y}$에 친화적인 말과 같습니다. 즉, 다음 차시에서는 제안함수를 받아들여 확률변수를 $y$로 변화시켜 샘플링을 합니다.
• Case 2: $\alpha \lt 1$
  • Acceptance가 1보다 작은 경우입니다. 이는 식 5의 중간변을에서 변수가 이동하는 방향이 $x\rightarrow{y}$에 친화적이지 못합니다. 즉, 다음 차시에서는 제안함수를 무시하고 상태변수를 $x$로 고정시키고 샘플링을 합니다.

여기까지 MH sampling 방식을 알고리즘으로 정리를 하면 다음과 같습니다.

• Step 1: 초기 확률변수($\theta_{old}$)를 설정한다
• Step 2: 다음 확률변수($\theta_{new}$)를 $Q(.)$을 통해 임의로 설정한다.
• Step 3: 식 5를 통해 Acceptance를 계산한다.
• Step 4: Acceptance를 1과 비교한다.
  • Case 1이면 $\theta_{old} {\leftarrow} \theta_{new}$
  • Case 2이면 $\theta_{old} {\leftarrow} \theta_{old}$
• Step 5: Step2~4까지 충분히 반복

필자가 간단하게 만들어본 Metropolis-Hasting algorithm 예제를 같이 살펴보도록 합시다.

MetroPolis-Hasting 튜토리얼 코드.

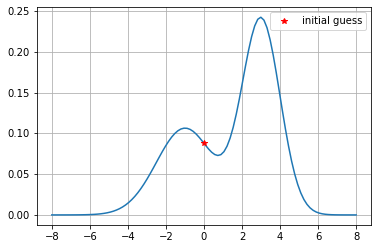
튜토리얼 코드니까 1D의 쉬운예제로 세팅했습니다. 우리는 위와 같은 분포의 확률분포값을 샘플링해서 구체적인 값을 얻고 싶습니다. 필자는 위 확률분포를 어떻게 세팅해서 정확히 얼마의 확률 값이다! 라고 말할 수 있지만 그게 현실상 불가능하기에 근사방식인 MCMC중 Metropolis-Hasting 알고리즘을 이용해 위 문제를 해결할 것입니다. 그림을 놓고 보자면 대략 $x=3$위치에서 확률분포가 크게 나타나므로 많이 샘플링이 될 것으로 추정됩니다.

붉은색 별표의 $x$좌표가 확률변수의 값, $y$좌표가 해당하는 샘플링 확률 $P(x)$입니다. 함수값이 대략 8% 로 예상됩니다.

이제, Metropolis-Hasting 함수를 코드로 작성해보겠습니다.

# Metro-polis hasting algorithm
def Metropolis_Hasting(x_old,x_new,function):
    '''
    x_old: original position
    x_new: newly suggested position
    function: sampling function --> we have to maximize
    '''
    # np.random.normal can be modified in your choice
    num = function(x_new)*np.random.normal(x_new,1)
    den = function(x_old)*np.random.normal(x_old,1)
    if den == 0:
        acceptance = 1
    else:
        acceptance = num/den
    
    if acceptance >= 1:
        result = x_new
    else:
        result = x_old
    return result

함수코드의 입력 인자는 순서대로 현재의 확률변수 위치$\theta_{old}$, 제안된 확률변수 위치$\theta_{new}$, 그리고 각 확률변수의 확률값을 구해줄 함수 혹은 시스템인 function입니다. num, den변수가 acceptance($\alpha$)를 구하기 위한 준비물로, 필자는 np.random.normal $\leftarrow$ Gaussian distribution을 이용해 $Q(.)$를 제안해주었습니다.

나머지 부분은 알고리즘의 흐름대로 작성하면 끝입니다. 이제 MH함수를 이용하는 샘플링 코드는 아래와 같습니다.

dev = 1
iter_num = 5000
record = np.zeros((iter_num,2))
x_old = 0
x_new = np.random.normal(x_old,dev)
for i in range(iter_num):
    x_old = Metropolis_Hasting(x_old,x_new,mixture_gaussian)
    record[i,0] = x_old
    record[i,1] = mixture_gaussian(x_old)
    x_new = np.random.normal(x_old,dev)

5000번을 반복 샘플링을 합니다.. 매 반복 차시마다 x_new라는 변수를 Gaussian distribution을 이용하여 새 위치로 제안해주었는데 독자 여러분은 알고 있는 특이한 확률분포를 이용해서 다른 방식으로 시도해봐도 재미있겠습니다.

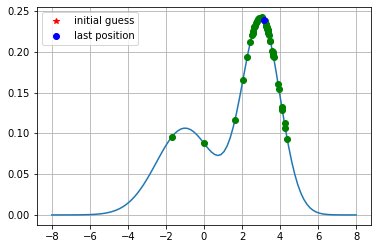
이렇게 해서 얻은 샘플링값의 그림입니다. 확률분포의 꼭대기, 즉 확률이 가장 높은 영역에서 샘플링된 횟수가 가장 많으며, 마지막으로 샘플링된 확률 변수값은 $x=3.1406407759393016$입니다. 얼추 예상한 바대로 샘플링이 잘되었지 않았나요?

이렇게 얻은 $\theta$를 머신러닝의 사전지식, 파라미터라고 생각해보면 주어진 데이터를 많이 관찰하여 제일 그럴싸한 확률분포를 가지는 변수로 추론을 한다고 여기면 될것이다. 제안된 임의의 함수를 평가하고 자신의 사전지식을 개량하는 방식으로 직관적으로 생각하면 된다.

맺음말

지금까지 우리가 원하는 확률분포 $P(\theta)$를 구하는 전략으로 MCMC방법과 그 구체적인 샘플링 방식으로 Metropolis-Hasting 알고리즘을 살펴보았습니다. 이 전략들은 사전지식과 주어진 데이터를 이용하여 사전지식을 바꾸는 베이지안 통계방식의 대표적인 예시입니다.

다음 포스팅에서는 회귀분석에서 쉽게 적용될수있는 Gaussian Process에 대해서 살펴보도록 하겠습니다. 혹시 설명이 이해가 안되거나 애매한 부분이 있으면 적극적으로 댓글 많이 부탁드리겠습니다!