글을쓰는 지금 재직하고 있는 회사에서 포커스를 두는 분야는 아니지만 한때 Reinforcement Learning에 대해서 많은 관심을 가지고 깊이까지는 아니지만 짤막하게 공부를 했었고다. 이전 포스팅에서 다룬 연구가 Reinforcement Learning을 응용한 바, 이전에 필자가 공부했던 RL도 정리해야 겠다는 필요성을 느꼈다. 그래서 RL의 기본 내용과 DQN, A2C까지의 알고리즘을 차차 진행해보고자 한다. 첫번째 여정으로 RL의 기본개념 부터 정리하겠다.
Reinforcement의 기본요소
Supervised learning, Unsupervised learning은 각각 {data,label}, {data}라는 확률분포를 이용해서 인공지능을 사람이 원하는 방식대로 학습하는 방식을 채택한다. 즉, 그 방식이 DNN처럼 parameteric 방식을 사용하던 Gaussian Process처럼 Non-parameteric method를 사용하던간에 $P(x)$에 의해서 학습의 결과가 좌지우지 되는 학습방식이다.
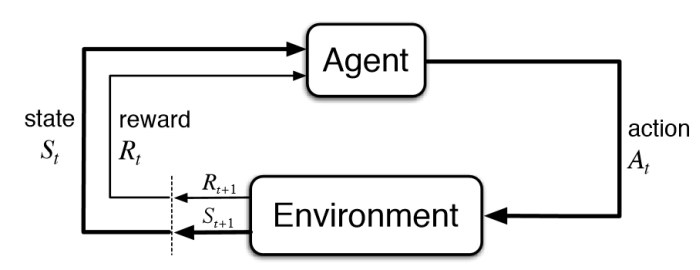
반면에, RL은 머신러닝의 큰 세 분류중에서 데이터라는 개념이 없는 학습방식이다. 그 대신 아래의 요소들이 RL의 학습방식을 주관하게된다.
- Agent: 학습을 하는 대상으로 직관적으로 생각되는 인공지능
- Action: Agent가 수행하는 행동을 의미
- Environment: 환경. Agent가 활동하는 영역
- State: 상태. Agent가 인식하는 Environment의 상황
- Reward: 보상. Agent가 취해야할 목표
RL의 기본 요소들은 위 그림에서 보이는 관계도를 그리고 있다. 행동의 주체인 Agent가 Environment로부터 state를 부여받고 최적의 Action을 취하면, 그에 대한 Envrionment의 반응으로 Reward를 부여받게된다. RL은 그 Agent가 Reward를 최대화 시키도록 주어진 환경에서의 Action을 적절히 선택하도록 만드는 방식이라고 요약할 수 있겠다. 위 그림의 순환구조를 Markov Decision Process(MDP)라고 명칭하며, RL은 또다른 표현으로 MDP를 해결하는 과정이라고 달리 표현 할 수 있다. 위 순환구조는 시행횟수가 계속해서 진행되는 과정이므로 시계열과정으로 문제풀이가 진행되며 ‘현재’와 ‘미래’라는 개념이 추가가 된다. 그래서 위 RL의 기본 요소 중 수식으로 표현할 부분을 이제부터 아래와 같이 표현하며 이야기하지 않은 두 가지 요소를 더하도록 하겠다.
- Action: $a_t$
- State: $s_t$
- State transition probability matrix: $P_{ss’}^{a}$
- Reward: $R_s^a=\mathbb{E}[R_{t+1} \vert S=s_t, A=a_t]$
- Discount factor: $\gamma \in [0,1)$
Action과 State에서 $t$는 몇회차때의 행동인지 나타내는 인덱스를 가리키는 것으로 설명을 줄인다. Reward는 위와 같이 표현하는데, t회차때의 state와 action을 취해지면 다음 차시에서 environment가 reward값을 제공하므로 $R_s^a$는 t+1차시때의 reward값의 기대값으로 이야기 하는 것이다. $P_{ss’}^{a}$는 agent가 현재 state($s$)상황에서 action($a$)을 취하면 환경이 다음 state($s’$)로 바뀌는 확률을 가리킨다. 이상적인 상황에서 environment의 모든 요소하나하나 다 알고있다면 $P_{ss’}^{a}$의 모든 값들을 파악 할 수 있지만 실질적으로는 그렇기에는 까다로운 부분과 굳이 생각하지 않아도 되는 경우들이 있다. 따라서 앞으로 우리가 마주할 문제는 대다수 $P_{ss’}^{a}$값이 1이라고 고정시켜놓고 봐도 무방할 것이다. 마지막으로 Discount factor $\gamma$는 현재의 $R_{t}$의 가치와 미래의 $R_{t+1}$ 가치를 구분시켜주는 요소이다. 직관적으로 생각하면 지금 바로 100만원의 보상을 받는 것과 10년뒤 미래에 100만원을 받는 것은 그 가치에 대한 차이가 확연히 나는것과 같은 이치다(할인율). 다시 말하자면, 100만원이라는 것이 10년의 시간이 흐름에 따라 가치가 상실하고, 그 상실한 가치의 비율이 바로 $\gamma$값이다.
RL의 목표
한 마디로 간단하다. Agent의 목표는 Reward를 최대화하는 action을 매 state마다 취하면 RL문제가 풀린 것이다. 우리가 Agent를 하여금 풀어야 할 문제인 Reward를 고찰해야할 필요가 있다. 현재시간 차시를 $t$라고 두면 Agent는 $R_{t+1}$만을 단순하게 최대화를 하는 것이 아니라 미래의 상황까지 모두 고려한 최종보상을 최대화 해야하는 것이다.
예시
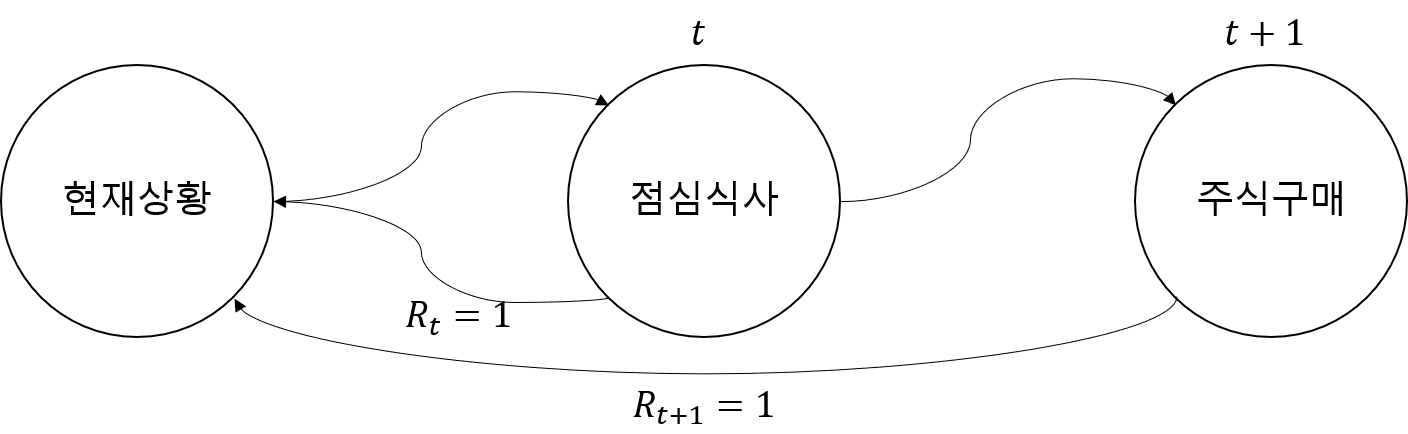
쉬운 예제로, 지금 수중의 1만원으로 점심을 사먹는 것도 Reward이고, 1만원으로 조금 더 미래에 10만원으로 불리는 주식을 구매하는 것도 Reward라면 Agent는 어떤 행동을 더 좋은 보상을 얻는다는 행동으로 간주할 것일까? 만약 지금 당장의 보상을 더 가치있게 여긴다면 Agent는 점심을 먹게될 것이고, 나중의 보상을 더 가치있게 여긴다면 Agent는 주식을 사게된다. 지금 당장의 보상을 가치있게 여긴다면 $\gamma$는 0에 가까운 값을, 미래의 보상을 현재의 보상만큼이나 귀하게 여긴다면 $\gamma$는 1에 가까운 값을 가져야 한다. 여기서 주의할 점은 $\gamma$는 1보다는 작아야 한다! 그렇지 않으면 MDP가 수렴하지 않아서 Agent가 해를 구하지 못하고 발산해버린다(참고링크). 다시 돌아와서 이렇게 현재 얻을 보상 $R_{t+1}$, 다음 순간에 얻을 보상 $R_{t+2}$, 그 다음 순간에 얻을 보상 $R_{t+3}$, … k번째 차시까지 해서 얻을 보상 $R_{t+k+1}$을 모두 고려해서 현재 평가한 최종보상($G_t$, RL분야에서는 return이라고 명명)은 아래 수식처럼 표현된다.
\(\begin{align} G_{t}&=R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \\ &=\sum_{k=0}^{\infty}{\gamma}^k{R_{t+1+k}}. \end{align}\) (1)
다시 1만원을 가지고 점심으로 해결하는 상황, 주식을 사는 상황을 비교해보자. 각자마다 다를 순 있겠지만 점심을 먹는다는 보상은 +1, 주식을 구매하는 보상도 +1이라고 동일하게 놓고 최종보상 $G_t$ return을 계산해보자.
- [$\gamma=0$] 점심식사를 선택한 agent의 $G_t$
- \(\begin{align}G_t &= R_{t+1}+\gamma{R_{t+2}} \\ &=1+0{\times}0. \end{align}\) (2)
- [$\gamma=0.99$] 주식구매를 선택한 agent의 $G_t$
- \(\begin{align}G_t &= R_{t+1}+{\gamma}R_{t+2}\\ &=0+0.99{\times}1. \end{align}\) (3)
식 (2)와 식 (3)을 비교했을때,return은 지금 당장 점심식사가 더 갚진 모습이므로 agent는 1만원을 들고 점심식사를 하러 행동을 할 것이다. 이 예시는 현재의 보상이 좋아보이는 선택을 하였지만, 그 이면에는 생각 가능한 미래까지 얻을 수 있는 보상을 모두 고려한 return을 비교하여 최적의 행동을 취하는 것이 RL의 목표가 된다. 독자들이 생각해보기 바란다 이 문제의 상황을 바꿔서 agent가 주식을 사도록 보상의 조건을 바꿔보자. 지금 당장 점심을 먹는 보상을 +0.7, 주식을 사는 보상이 만약 +0.9라면 agent는 어떤 행동을 취하게 될까? 각각의 반대대는 보상의 정도는 1에서 해당 값을 제한다고 가정하라.
Value function & Action-value function
위 예시 문제를 통해 agent가 받을 최종보상을 살펴보았다. 이 최종보상을 RL의 agent가 구체적으로 계산할수 있도록 보자. 가치함수 $V(s)$라는 용어가 등장하는 데 글로 풀어쓴 정의로 ‘현재 state에서 장기 미래시점까지 보는 최종 가치’이며 수식으로 표현하면 아래와 같다.
\(V(s)=\mathbb{E}[G_t\vert S_t=s].\)(4)
Return의 기대값이 바로 $V(s)$이며, RL은 $V(s)$를 Maximizing하는 과정으로 풀이 할 수 있겠다. 가치함수는 해당 state에서 모든 action을 다 고려했을때 얻을수 있는 기대값으로 정의되며 식 (4)를 아래와 같이 달리 표현된다.
\(\begin{align} V_{\pi}(s) &= \mathbb{E}_{\pi}[G_t\vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma \left( {R_{t+2}}+\gamma{R_{t+3}}\cdots \right) \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1} \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1}) \vert S_t=s] \\ \end{align}.\)(5)
식 (5)와 같이 현재 state의 value function을 안다는 것은 다음 state의 value function을 알아야하는 점화식의 표현이 된다. 동적계획법(Dynamic programming)의 방식으로 큰 문제를 작은 문제로 분할해서 해결하는 방식이 RL에 적용되는 방식을 고려해야한다. 아래첨자 $\pi$가 등장했는데 이는 정책 Policy라고 명명하며 어떤 action을 취할지 주관하는 action의 probability이다.
식 (4)와 식(5)는 가치함수를 다뤘고, 지금까지는 agent가 취하는 action에 대해서 구체적으로 생각하지 않은 보상을 이야기했다. 엄밀하게는 agent가 모든 action을 다 고려한 보상에 대한 가치를 분석한 것이다. 이제는 action까지 같이 고려한 보상에 대해서 분석하고자한다. 액션-가치함수, 달리 표현해서 Q-함수라고 말하며 $Q_{\pi}(s_t,a_t)$로 작성한다. $Q_{\pi}(s_t,a_t)$와 $V_{\pi}(s_t)$와의 관계는 다음과 같다.
\(V_{\pi}(s_t)=\sum_{a_t \in \mathcal{A}}{\pi(a_t \vert s_t) Q_{\pi}(s_t,a_t)} .\) (6)
즉, 모든 action에 대해서 policy와 Q-함수의 곱이 곧 최종 가치함수화 동일하다. 이 관계를 식(5)에 대입해서 특정 action에 대한 Q-함수의 값을 표현하면 다음과 같다.
\(\begin{align} Q_{\pi}(s,a) &= \mathbb{E}_{\pi}[G_t\vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma \left( {R_{t+2}}+\gamma{R_{t+3}}\cdots \right) \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1} \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma Q_{\pi}(S_{t+1},A_{t+1}) \vert S_t=s, A_t=a] \\ \end{align}.\)(7)
Reinforcement Learning API
이론이 굉장히 길었다. 첫번째 RL포스팅의 이론 부분은 이쯤 줄이도록 하고 앞으로 우리가 꾸준히 살펴볼 RL연구 전용으로 많이 애용되는 OpenAi Gym API를 살펴보고자 한다. OpenAi Gym의 정보를 얻고 싶으면 OpenAi 위키 링크와 Gym github 링크를 참조해주기를 바란다.
- 설치 및 호출
# 설치 !pip install gym # 라이브러리 호출 import gym - gym 간단 가이드 gym의 환경은 매우 많다. 카트 폴, 마운틴 카, 택시, 아타리 벽돌깨기, 그리고 마리오까지 다양한 agent를 학습시킬수 있는 환경은 많지만 한번에 환경을 다 소개할수는 없고 포스팅 마다 적절한 환경을 가지고 와서 설명하겠다. 첫번째로 가장 많이 이용되는 ‘카트폴’ 문제를 보겠다.
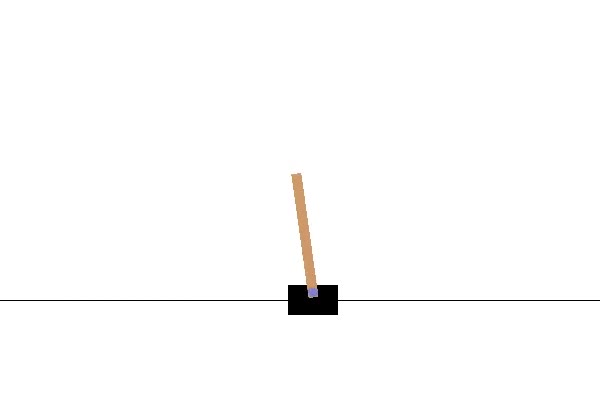
이 RL의 목적은 카트를 화면밖으로 넘기지 않으면서 세워진 봉을 쓰러트리지 않은채 오랫동안 서있게 유지시키는 것이다.
- 카트폴 환경 호출 및 초기 상태불러오기
gym의 ‘make’로 카트폴 환경을 호출하고, ‘reset’으로 초기 상태를 불러오기를 수행한다. render를 이용해 상태를 시각화 할 수 있다. 학습이 다 된 이후에 render를 이용해 확인할 것이다.
import gym env = gym.make('CartPole-v1') state = env.reset() # env.render() 현재 환경을 사람이 보도록 렌더링 - 환경 분석
매번 새로운 환경을 마주할때 마다 어떤 액션을 취할수 있는지 분석해야한다. 미리 알고 있다면 굳이 하지 않아도 되는 작업이다.
print(help(env.unwrapped))출력화면 일부
| Observation: | Type: Box(4) | Num Observation Min Max | 0 Cart Position -4.8 4.8 | 1 Cart Velocity -Inf Inf | 2 Pole Angle -0.418 rad (-24 deg) 0.418 rad (24 deg) | 3 Pole Angular Velocity -Inf Inf | | Actions: | Type: Discrete(2) | Num Action | 0 Push cart to the left | 1 Push cart to the right | | Reward: | Reward is 1 for every step taken, including the termination step |- 상태(observation): 차원은 4로써 각각의 인덱스는 [위치, 속도, 폴의 각도, 폴의 각속도]로 구성.
- 액션(Actions): 2차원으로 [왼쪽이동, 오른쪽이동]으로 구성.
- 보상(Reward): 매 차시때마다 +1. 즉, 오랫동안 버틸수록 보상은 계속 쌓인다.
- 샘플 RL진행
아직 우리는 RL의 이론중에서 개념밖에 이해하지 못해서 실제 RL을 학습해서 카트폴 문제를 해결할수는 없지만 gym에서는 샘플 액션을 받아올수 있으므로 샘플대로 agent를 환경에 진행시켜보겠다.
total_reward = 0 for _ in range(100): # 100회 액션수행차시를 관찰한다. env.render() action = env.action_space.sample() # gym의 샘플 액션을 취한다 observation, reward, done, info = env.step(action) # 에이전트가 샘플 액션을 수행하고, 다음환경, 보상, 종료여부, 기타 정보를 얻는다 total_reward += reward if done: observation = env.reset() # 종료되었다면 다시 환경을 리셋한다 print(f'Episode finished! Total reward: {total_reward}') total_reward = 0 env.close()100회 동안의 액션 수행을 관찰하며 육안으로 보기위해 렌더링 옵션을 열었다.
- env.action_space.sample()을 이용해서 샘플 액션을 취하고,
- env.step(action)을 이용해서 환경에 액션을 수행한다. 출력은 주석에 달아놓은 정보들이다.
- 종료여부가 달성되면 새로 환경을 열고 봉이 쓰러지기 전까지 얼마의 보상을 획득했는지 값을 출력한다.
대략 필자가 위 코드대로 수행하면 봉이 쓰러지기전까지 대략 10초반~20이내의 보상을 환경으로 부터 얻는값을 확인하였다. 이제 앞으로 여러 강화학습 문제를 마주하면서 저 보상값을 최대로 하는 값을 얻는 방식에 대해서 공부할 것이며, 최종적으론 특별히 종료가 되기전까지는 카트를 절대 쓰러트리지 않는 agent를 만들도록 하겠다.
다음 포스팅에선, Bellman equation을 보다 상세히 살펴보고 agent의 학습이란 개념을 본격적으로 살펴보도록하겠다. RL은 육안으로 보기에는 굉장히 쉬우나 용어에 대한 이해가 부족하면 나중에 굉장히 고생하고 헷갈릴 여지가 많으니 처음부터 개념을 올바르게 이해하는게 중요하다!