혹시 강화학습에 대한 기초 개념을 모른다면 이전 포스팅부터 보고 와주기를 바란다. 이번 포스팅에선 지난 포스팅에 이어서 Bellman equation의 이론과 그에 따른 agent의 최적화 방식을 조금 더 면밀히 살펴보고, 그럴싸한 강화학습 문제를 풀어보도록 하겠다.

Bellman equation

Bellman equation은 특별한 것은 아니고, 사실 지난 포스팅의 Value function과 Action-Value function을 전개한 식이 바로 Bellman equation이다. 하지만 그 이면에 더 세세한 사항들에 대해서 고려할 부분이 많기에 따로 챕터를 잡아 설명한다.RL은 일종의 Markov Decision Process를 푸는 과정과 같으며, 그 알고리즘은 일종의 동적계획법(Dynamic Programming)이라고 먼저 언급했었다. 최종보상을 최대화 하는 과정은 현재의 상태와 액션 $s_t, a_t$로부터 Value function, 혹은 Action-Value function(이하, Q-function으로 명명)을 미래의 상태와 액션 $s_{t+1}, a_{t+1}$로 쪼개어 수식으로 전개해서 푸는 과정을 다시 한번 보자.

Value function
- $\begin{align} V_{\pi}(s) &= \mathbb{E}_{\pi}[G_t\vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma \left( {R_{t+2}}+\gamma{R_{t+3}}\cdots \right) \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1} \vert S_t=s] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1}) \vert S_t=s] \\ \end{align}.$(1)
Q-function
- $\begin{align} Q_{\pi}(s,a) &= \mathbb{E}_{\pi}[G_t\vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma{R_{t+2}}+\gamma^2{R_{t+3}}\cdots \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma \left( {R_{t+2}}+\gamma{R_{t+3}}\cdots \right) \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1} \vert S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[R_{t+1}+\gamma Q_{\pi}(S_{t+1},A_{t+1}) \vert S_t=s, A_t=a] \\ \end{align}.$(2)

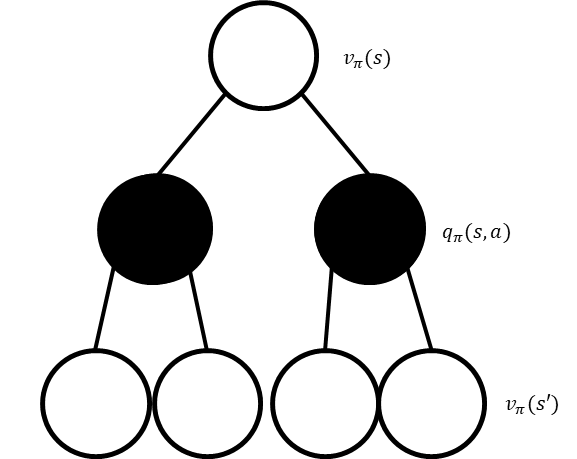
지난 포스팅에서도 그랬지만 말과 수식으로만 설명하려니 한계가 느껴지는 것 같다. 그래서 Value function, Q-function, 그리고 두루뭉술하게 넘어갔던 Policy($\pi$)를 그림이 포함된 일련의 과정과 함께 살펴보자.

value_q

그림의 투명한 원은 Value function의 값, 검은 원은 Q-function의 값을 의미한다. 또 environment로부터 agent가 취할수 있는 action 옵션은 단 두 가지로 가정하여 Q-function으로 나가는 경로가 두 갈래로 표현되었다. 현재 state에서의 value는 모든 action에 대한 return값을 계산하지만, Q-function은 현재 $s$중에서도 특정한 $a$에 각각에 대한 return값을 계산하는 것을 고려한다. 따라서, 흰색원으로 부터 검은색 원으로 값이 분화될때 그 갈래로 나뉘는 확률이 바로 policy($\pi)이며, 특정 action이 나오는 확률을 의미한다. 이 과정을 종합하여, Value function과 Q-function간의 관계는 아래와 같다

$V_{\pi}(s)=\sum_{a \in \mathcal{A}}{\pi(a \vert s) Q_{\pi}(s,a)}.$(3)

q_value

현재 state에서 다음 state로 넘어가는 상황에서의 Q-function과 Value function간의 관계는 위와 같다. 수식으로 표현된 문자가 혼용되어 굉장히 독자들에게 미안하지만 작성의 편의를 위해서 양해를 바란다. 현재 state와 action을 $s,a$로, 미래 state와 action을 $s’, a’$로 표현함을 미리 밝힌다. $s \rightarrow s’$로 가는 것은 agent가 $a$ action을 취했다는 의미가 된다. 우리가 간과하기 쉬운 부분이 있는데 environment에서 $a$를 취했다고 예상되는 구체적인 $s’$가 생기는 것이 아니다. 실제로 environment의 정보를 완벽하게 아는 agent는 없다. 예를 들어 신호등의 직진신호를 받아 차를 출발했는데 무사히 잘 출발하리라는 보장을 할 수 없다. 왜냐하면, 갑자기 차도를 향해 뛰어드는 무단보행자나 앞차가 신호를 보지 못하고 출발하지 못해서 나도 출발 할 수 없는 상황에 마주하기 때문이다. 이는 우리가 앞서서 State transition probability, $P_{ss’}^{a}$를 언급했었던 부분이다. 즉, 현재 $a$를 취한다고 해서 $s \rightarrow s’$의 확률이 1이 아닐수도 있음을 고려 해야한다. 위 그림은 예기치 못한 경우로 분화되는 케이스를 하나를 더 두어 $s’$가 두 가지 케이스로 나뉠 수 있음을 보여준다. 따라서, Q-function을 미래의 Value function로 표현하면 다음과 같다.

$Q_{\pi}(s,a) = R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{\pi}(s').$(4)

식 (4)에선 미래의 state로 진행됨에 따라 environment로 부터 reward $R_{ss’}^{a}$를 받는 부분을 놓치지 않도록 유의하자.

이제 Value-function $\rightarrow$ Q-function의 관계와 Q-function $\rightarrow$ Value-function의 관계를 종합하여, Value-function과 Q-function 각각의 동적계획법 형태로 풀이된 Bellman equation으로 표현 할 수 있다.

Bellman equation style Value-function

value_q_value

$\begin{align} V_{\pi}(s)&=\sum_{a \in \mathcal{A}}{\pi(a \vert s) Q_{\pi}(s,a)} \\ &=\sum_{a \in \mathcal{A}}{\pi(a \vert s)}\left\{R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{\pi}(s') \right\}. \end{align}$(5)

Bellman equation style Q-function

q_value_q

$\begin{align} Q_{\pi}(s,a)&= R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{\pi}(s') \\ &=R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a}\left\{ \sum_{a' \in \mathcal{A}}{\pi(a' \vert s') Q_{\pi}(s',a')} \right \}. \end{align}$(6)

Bellman optimality equation

$s \rightarrow s’$에서 모든 $a$경우를 다 비교분석한 방식이 바로 Bellman equation이다. 식 (5)와 (6)이 모두 모든 $s$의 경우와 $a$의 상황을 다 고려하고 문제를 푸는 방식인데 이렇게 문제를 접근하면 계산량에도 문제가 있고 굳이 고려하지 않아도 되는 부분에 대해서 쓸데없이 고려하는 문제가 발생한다. 실질적인 대안으로 해당 상황에 대해서 ‘최적’의 행동을 목표로 하는 것이 RL의 방식이다. 다시말해 ‘최적’의 행동을 취하는 방법과 모든 행동의 경우를 다 고려하겠다는 전략이 바로 RL과 MDP의 문제해법방식의 결정적 차이이다. 그렇다면 최적의 행동을 취하는 agent의 $\pi$를 수식으로 표현해보자.

$\pi_{*}(a \vert s)= \begin{cases} 1, & \text{for } a=\text{argmax}_{a \in \mathcal{A}}Q_{*}(s,a)\\ 0, & \text{for otherwise}. \end{cases}$ (7)

식 (7)에서부터 등장하는 아래첨자의 * 표시는 Bellman optimality equation을 의미한다. 이제는 $\pi$의 분포를 모든 $a$에 대해서 고려하는 것이 아닌 최고의 Q_function을 출력하는 $a$에 대해서만 고려하겠다는 의미를 가지고 MDP 해법인 Bellman equation을 Bellman optimality equation으로 다음과 같이 변형된다.

value_opt

Bellman equation 챕터에서 나온 그림과 차이가 있다면 갈래길에서 부채꼴이 하나가 추가되었는데 이 의미는 ‘갈림길중 최대값을 선택’한다는 의미를 내포하고 있다. 따라서, 식 (3)을 Bellman optimality equation으로 표현하면 다음과 같다.

$V_{*}(s)=max_{a \in \mathcal{A}}{Q_{*}(s,a)}.$(8)

q_opt

Q-function에서 value function으로 넘어가는 단계는 딱히 변할수 있는 부분이 없다. 이는 agent가 어떤 행동을 취하는 지의 문제가 아니라 environment가 어떤 $s$를 주는지에 결정된다. 따라서 식 (4)의 Bellman optimality equation은 다음과 같이 바뀐다.

$Q_{*}(s,a) = R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{*}(s').$(9)

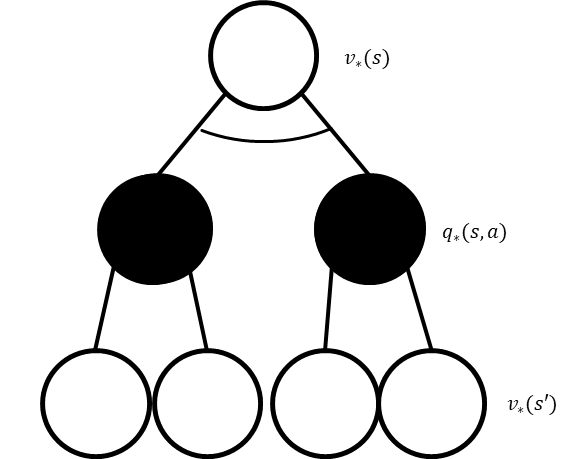
value_q_value_opt

마지막으로 $s \rightarrow s’$는 두 식을 합쳐서 아래와 같이 표현된다.

$\begin{align} V_{*}(s)&=max_{a \in \mathcal{A}}{Q_{*}(s,a)} \\ &=max_{a \in \mathcal{A}}\left(R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{*}(s') \right). \end{align}$(10)

Practice(1): Bellman equation, 4x4 grid value

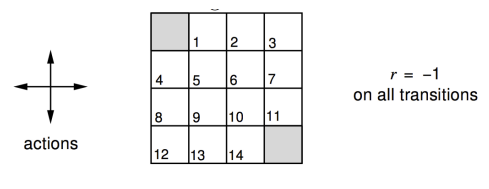
David_silver_lecture

David silver 교수님의 Reinforcement learning 강의에서 나온 문제, 4x4 격자의 최적경로 검색 문제를 풀이해보자. 문제의 상황 설정은

좌측 최 상단, 우측 최 하단 지점은 격자 검색이 종료되는 지점이다.
- 한번 행동을 개시하면 reward는 -1의 보상을 받는다.
- $\gamma$는 1로 설정.
$\pi$는 어떤 $s$에서든 사방향으로 모두 동일한 확률분포를 가진다.
- $\pi(a \vert .)= \begin{cases} \frac{1}{4}, & \text{for } a=left \\ \frac{1}{4}, & \text{for } a=up \\ \frac{1}{4}, & \text{for } a=right \\ \frac{1}{4}, & \text{for } a=down. \end{cases}$ (11)
$s \rightarrow s’$는 policy가 의도한대로 움직인다. 즉, $P_{ss’}^{a}$는 1로 고정 되어있다.

$\gamma$를 1로 둘 수 있는 이유는 해당 문제에서는 어느 경로를 가더라도 문제가 종료되는 지점이 있으므로 문제가 발산하지 않기 때문에 가능하다. 덧붙여 모서리, 귀퉁이 같은 지점에서 특정 방향으로 더 이상 움직일수 없으면 $s’ \leftarrow s$이다. Bellman equation으로 4x4격자의 16개 지점에서 최종 Value-function이 어떻게 연산되는지 구해보겠다.

시작단계

모든 격자의 가치는 주어져있지 않다. 모두 0으로 고정되어 있으므로 따로 계산할 필요는 없다.
```
 import numpy as np

 # initializing
 old_value = np.zeros((4,4))
 new_value = np.zeros((4,4)) 
 policy = {'up':0.25,'down':0.25,'left':0.25,'right':0.25}
```
$s$와 $s’$에 대한 value가 update되는 과정이 필요하므로 new_value, old_value로 두 변수를 만들고 swap을 진행할 것이다. 또한, $\pi$는 격자의 경계지점 문제가 있기 때문에 딕셔너리로 형태로 이름을 명확하게 집어넣었다. 이 부분은 계속한 코드에서 더 언급하겠다.
첫번째 진행

첫번째 보상이 진행되었다. 식 (5)를 이용해 Value-function의 $s’$의 상황을 고려하고 업데이트를 진행하면 된다. 초기 Value-function값은 모두 0으로 고정되어있으므로 특별히 어려울 부분은 없다.

$\begin{align} V_{\pi}(s) &=\sum_{a \in \mathcal{A}}{\pi(a \vert s)}\left\{R_{s}^{a}+\gamma \sum_{s' \in S}P_{ss'}^{a} V_{\pi}(s') \right\} \\ &=-\sum_{a \in \mathcal{A}}{\pi(a \vert s)} \\ &=-1. \end{align}$(12)
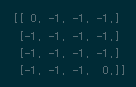
```
 # 1st step
 dummy_list = []
 for key,value in policy.items():
     dummy_list.append((-1+old_value)*value)
 dummy_list = np.sum(np.array(dummy_list),axis=0)
 new_value = dummy_list
 new_value[0,0],new_value[-1,-1] = 0,0
 old_value = new_value
```
여기까지는 경계지점에 대해서 딱히 고려할 부분이 없다. 왜냐하면 격자내 모든 Value-function값이 0으로 설정되어있기에 특별히 경계지점을 생각하지 않아도 계산이 올바르게 진행된다.

순차적 진행

t번째 보상이 진행되었다. 이제는 점화식처럼 첫번째 계산을 진행한것처럼 반복수행을 진행하면 된다. 단, 모서리와 경계면쪽에서의 계산에 유의하면서 점화식형태로 반복시행하자!

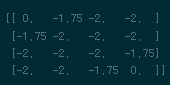
2nd_bellman

$\vdots$

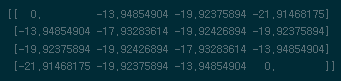
inf_bellman

 # 2nd step -> k_iteration 원하는 만큼
 dummy_list = []
 mid_term = np.zeros((4,4))
 for key,value in policy.items():
     # upper bound
     if key == 'up':
         mid_term[1:,:] += (-1+old_value[:-1,:])*value
         mid_term[0,:] += (-1+old_value[0,:])*value
     # down bound
     elif key == 'down':
         mid_term[:-1,:] += (-1+old_value[1:,:])*value
         mid_term[-1,:] += (-1+old_value[-1,:])*value
     # left bound
     elif key == 'left':
         mid_term[:,1:] += (-1+old_value[:,:-1])*value
         mid_term[:,0] += (-1+old_value[:,0])*value
     # right bound
     else:
         mid_term[:,:-1] += (-1+old_value[:,1:])*value
         mid_term[:,-1] += (-1+old_value[:,-1])*value
     dummy_list.append(mid_term)
 dummy_list = np.mean(np.array(dummy_list),axis=0)
 new_value = dummy_list
 new_value[0,0],new_value[-1,-1] = 0,0
 old_value = new_value

반복 진행시점부터 경계지점에 대해서 고려해줘야한다. Value-function이 반복 진행됨에 따라 더 이상 0으로만 고정되어있지 않으므로 경계선에서 agent가 진행 할 수 없는 움직임을 취하는 옵션이 있다면 가만히 있어야 한다는 제약을 걸어줘야 한다. 이 부분을 mid_term이라는 변수를 통해서 고려해줬으며 dummy_list변수에서 평균값을 취해줬는데 1회차 step과는 달리 반복 진행차부터는 4방향에 대해서 계속해서 누적합이 발생되었기 때문에 이를 모든 $a$에 대해서 공정하게 나눠주야 한다.

Bellman equation을 해결한 agent를 4x4격자내 임의의 위치에 옮겨 놓으면 가만히 있으라는 action의 옵션이 없으니, 현재 agent의 위치에서 가장 Value값이 큰 인접지역으로 이동, 그 후 최고 값으로 이동… 반복하여 상황 종료되는 좌상단, 우하단의 지점으로 최대한 빨리 이동하려는 action을 취하게 될 것을 표로 확인 할 수 있다.

Practice(2): Bellman optimality equation, 4x4 grid

위 4x4 grid 문제상황과 하나의 문제상황만 다르게 설정된다.

좌상단으로 부터 우하단까지로 agent가 최단 경로를 검색한다.

최적의 policy를 구해야하는 문제로 Bellman optimality equation을 사용하여 최단경로를 검색한다. 인간은 직관적으로 우측3번,하단3번을 무작위로 조합하면 최단경로를 검색할수 있다고 직관적으로 알 수 있지만 직관이 없는 agent가 옆길로 새지않고 목적지까지 이동하는 모습을 이론을 통해서 풀어보도록 하겠다.

시작단계

시작단계는 역시 앞선 예제와 같이 사전에 아무정보도 없으니 모든 가치는 0으로 진행된다. Optimality action만 취해야하니 policy를 따로 정의내리지 않겠다.
```
 # initializing
 old_value = np.zeros((4,4))
 new_value = np.zeros((4,4)) 
```
첫번째 진행

Optimal Value-function은 식 (10)을 이용해서 업데이트된다. 시작단계에서 Value-function이 0으로 시작되었으니 특별히 고려할 부분은 없다.
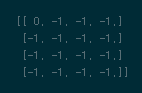
```
 # 1st step
 new_value = -1+old_value
 new_value[0,0]=0
 old_value = new_value
```

순차적 진행

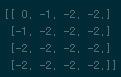
2nd_bellman_opt

$\vdots$

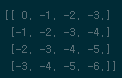
inf_bellman_opt

t번째 차시가 진행되었다. 식 (10) 반복수행을 통해서 계산을 수행한다. 아래 코드블럭을 7번정도 반복하면 Bellman optimality equation이 수렴되어 문제가 최종 해결된다.

 for row in range(4):
     for col in range(4):
         # top-left corner -> always zero
         if row == 0 and col == 0:
             pass
         # top-mid   
         elif row == 0 and col != 3:
             new_value[row][col] = max((-1+old_value[row][col-1]),(-1+old_value[row+1][col]),(-1+old_value[row][col+1]),(-1+new_value[row][col]))
         # top-right corner 
         elif row == 0 and col == 3:
             new_value[row][col] = max((-1+old_value[row][col-1]),(-1+old_value[row+1][col]),(-1+new_value[row][col]))
         # left-mid
         elif col == 0 and row != 3:
             new_value[row][col] = max((-1+old_value[row+1][col]),(-1+old_value[row][col+1]),(-1+old_value[row-1][col]))
         # left-bottom corner
         elif col == 0 and row == 3:
             new_value[row][col] = max((-1+old_value[row-1][col]),(-1+old_value[row][col+1]),(-1+new_value[row][col]))
         # bottom-mid
         elif row == 3 and col != 3:
             new_value[row][col] = max((-1+old_value[row-1][col]),(-1+old_value[row][col-1]),(-1+old_value[row][col+1]),(-1+new_value[row][col]))
         # bottom-right corner
         elif row == 3 and col == 3:
             new_value[row][col] = max((-1+old_value[row-1][col]),(-1+old_value[row][col-1]),(-1+new_value[row][col]))
         # right-mid
         elif col == 3 and row != 3:
             new_value[row][col] = max((-1+old_value[row-1][col]),(-1+old_value[row][col-1]),(-1+old_value[row+1][col]),(-1+new_value[row][col]))
         # else
         else:
             new_value[row][col] = max((-1+old_value[row-1][col]),(-1+old_value[row][col-1]),(-1+old_value[row+1][col]),(-1+old_value[row][col+1]))
 old_value = new_value        

모든 경계지점에서 $a$의 선택지가 달라진다. 따라서 하나의 grid에서 생각할수 있는 모든 $a$에 대해서 경우의 수를 다 따진다. 주석처리된 부분을 유의하면서 maximum value를 구할수 있도록 다음과 같이 구성한다. 7번 정도면 수렴된다.

Bellman optimality equation을 모두 해결하면 agent를 4x4격자내 좌상단 위치에서 부터 특정 임의의 위치까지 이동할때 소모되는 일종의 비용을 확인 할 수 있다. 이를 통해 특정위치까지 이동할때 왔던길을 되돌아 가지않고 최단경로로 이동하는 모습을 육안으로 확인 할 수 있다.

이번 포스팅에서는 Bellman equation과 Policy가 일정하게 유지되는 상황에서 최적선택을 하는 튜토리얼까지 살펴보았다. 다음 포스팅에서 동적계획법(Dynamic Programming)을 넘어 agent가 $a$를 주도적으로 선택하고 $\pi$를 주도적으로 업데이트를 하는 RL을 이야기해보겠다. 튜토리얼에 해법 전 코드는 여기 jupyter notebook링크를 통해 확인하기 바란다.

Hyunseok Hwang ML 연구노트

About Writing Contact

Reinforcement Learning_[2]

Bellman equation

Bellman optimality equation

Practice(1): Bellman equation, 4x4 grid value

Practice(2): Bellman optimality equation, 4x4 grid

Reinforcement Learning_[2]

Bellman equation

Bellman optimality equation

Practice(1): Bellman equation, 4x4 grid value

Practice(2): Bellman optimality equation, 4x4 grid

You may also enjoy:

Reinforcement Learning_[5]

Reinforcement Learning_[4]

Reinforcement Learning_[3]